33. Линейный интеграл вектора. Циркуляция векторного поля

Пусть поле - непрерывное векторное поле, (L) – кусочно гладкая кривая с выбранным на ней положительным направлением (ориентированная кривая).

Определение 1. Линейным интегралом (обозначается L) вектора вдоль ориентированной кривой (L) называется криволинейный интеграл

(1.7)

Для линейного интеграла справедливы следующие формулы:

(1.8)

=.

Если поле есть силовое поле , то линейный интеграл (1.7) дает величину работы этого поля вдоль линии (L). Вычисление линейного интеграла в зависимости от задачи может быть проведено по одной из формул “списка” (1.8).

Определение 2. Циркуляцией (обозначается Ц) векторного поля называется линейный интеграл по замкнутой ориентированной кривой (L):

. (1.9)

За положительное направление обхода замкнутой кривой (L) берется то, при котором область, ограниченная кривой, лежит под левой рукой.

Пример 1. Найти линейный интеграл вектора вдоль дуги (L) винтовой линии от точки A пересечения линии с плоскостью Z=0 до точки В пересечения с плоскостью Z =1.

Решение. Имеем по последней формуле из списка (1.8): . Точке A соответствует значение параметра T =0, точке B – значение и, таким образом, .

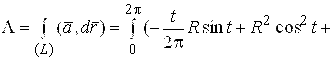
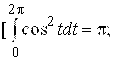
Пример 2. Вычислить работу силового поля вдоль отрезка прямой, проходящей через точки и .

Решение. Работа .

Запишем канонические уравнения прямой .
Отсюда ; параметры . Вычислим работу:
.

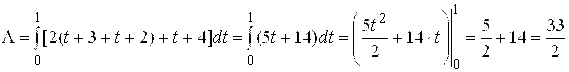Пример 3. Вычислить циркуляцию поля вдоль эллипса .

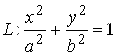Решение. Имеем по формуле (1.9) и (1.8): .
Запишем параметрические уравнения эллипса: . Вычисляя Dx и Dy, получим: 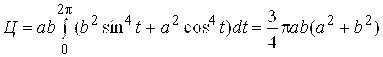- здесь использовано, что 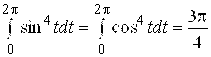(вычисление этих интегралов проводится с помощью понижения степени подынтегральной функции).

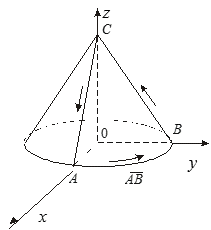
Пример 4. Вычислить циркуляцию векторного поля вдоль линии L, полученной пересечением конуса с координатными плоскостями (см. рис.4).

Рис. 4.

Решение. Линия L состоит из двух отрезков BC и CA, расположенных на координатных плоскостях Oyz и Oxz соответственно, и дуги окружности . Для циркуляции имеем: .1) На отрезке BC имеем: . Следовательно, . 2) На отрезке CA имеем: . Следовательно, . 3) На дуге AB окружности имеем: и =. Искомая циркуляция поля равна нулю.

Пример 5. Вычислить циркуляцию векторного поля вдоль линии , .

Решение. Имеем: . Линия L есть эллипс, получающийся в результате сечения цилиндра плоскостью . Найдем параметрические уравнения этой линии. Проекция любой точки этой линии на плоскость Oxy находится на окружности . Отсюда, полагая , найдем, что . Для Z из уравнения получим: . Таким образом, . Находим отсюда: , и для циркуляции запишем определенный интеграл: .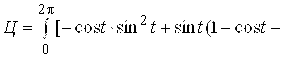

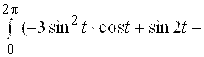
< Предыдущая		Следующая >