35. Ротор (вихрь) векторного поля

Пусть поле - дифференцируемое поле (то есть проекции вектора поля на оси координат являются дифференцируемыми функциями).

Определение. Вихрем векторного поля (обозначается rot) называется вектор, проекция которого на произвольный вектор определяется как предел отношения циркуляции поля по некоторому контуру (L), содержащему точку M, и лежащему в плоскости, перпендикулярной вектору , к площади области, ограниченной этим контуром, при условии, что этот контур стягивается в точку M, а площадь области (S) стремится к нулю:

. (1.13)

В трехмерном пространстве через декартовы прямоугольные координаты вектора выражается следующим образом:

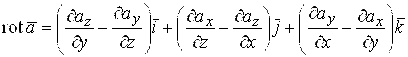, (1.14)

Или в удобной для запоминания символической форме

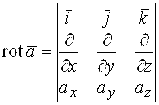. (1.15)

Теорема Стокса. Пусть координаты вектора + непрерывны и имеют непрерывные частные производные. Тогда циркуляция векторного поля по замкнутому контуру (L) равна потоку вихрей поля через произвольную поверхность (S), натянутую на этот контур:

. (1.16)

Предполагается, что ориентация контура (L) и поверхности (S) согласованы: при положительном обходе контура нормаль направлена от “ног к голове”.

Свойства ротора: 1) ; 2) .

Определение. Векторное поле называется безвихревым в данной области (V), если .

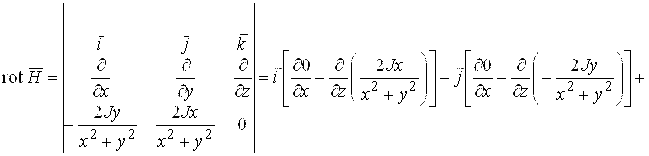
Пример 1. Найти ротор поля вектора напряженности магнитного поля .

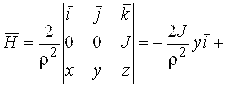
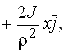
Решение. Вектор в координатной форме: . Вычислим ротор по формуле (1.15):

+ -

- поле напряженности - безвихревое поле.

Пример 2. Вычислить циркуляцию вектора по контуру 1)непосредственно, 2)по теореме Стокса.

Решение. 1)Контур (L) – окружность радиуса , лежащая в плоскости
Z =3 (см. рис.5).

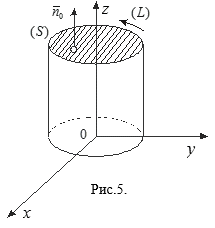
Выберем ориентацию на ней, как указано на рисунке. Параметрические уравнения линии , так что , . Для циркуляции вектора имеем: 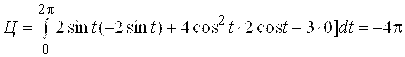. 2)Для вычисления циркуляции по теореме Стокса выберем какую-нибудь поверхность (S), натянутую на контур (L).Естественно в качестве (S) взять круг, имеющий линию (L) своей границей. Согласно выбранной ориентации контура нормаль к кругу необходимо взять равной . Вычислим ротор: .
По теореме Стокса
.

Задачи для самостоятельного решения

Найти векторные линии плоских векторных полей:

1.; 2. ; 3. ; 4.;

5..

Найти векторные линии:

6. ; 7. , где ;

8. ; 9., ;

10.; 11.; 12.;

13., Где - Постоянные векторы.

Найти векторные линии, проходящие через заданную точку:

14., ; 15., .

Вычислить поток векторного поля, используя поверхностный интеграл первого рода:

16. , (S): верхняя сторона треугольника, ограниченного плоскостями , .

17. , (S): внешняя сторона параболоида , ограниченного плоскостью ;

18. , : боковая поверхность кругового цилиндра , ограниченного плоскостями ;

19. , (S): внешняя сторона части параболоида , расположенной в первом октанте;

20. , (S): полная поверхность конуса , ограниченного плоскостью ;

21. , (S): замкнутая поверхность, ограниченная параболоидом и плоскостью Z = 0;

22. , (S): полная поверхность пирамиды, ограниченной плоскостями , , , ;

23. , (S): сфера .

Вычислить поток, используя метод проектирования на все три координатные плоскости.

24. , (S): верхняя сторона круга, вырезанного конусом на плоскости

25. , (S): верхняя сторона треугольника, полученного пересечением плоскости с координатными плоскостями;

26. , (S): часть плоскости , ограниченная окружностью , в направлении орта .

Определить поток поля, используя формулу Гаусса-Остроградского:

27. , (S): произвольная кусочно гладкая замкнутая поверхность;

28. , (S): поверхность куба , , ;

29. , (S): сфера ;

30. , (S): часть параболоида , отсекаемая плоскостью ; в отрицательную сторону оси Ox;

31., (S): поверхность тела , , ,

;

32. , (S): поверхность тела , ;

33. , (S): ;

34.;

35. .

Найти линейный интеграл вектора на плоскости:

36. верхняя половина эллипса 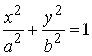от точки A(A,0), до точки B(-A,0);

37. а) отрезок прямой OB; б) дуга параболы ; в) дуга параболы ; г) ломаная OAB, где A(1,0); д) ломаная OCB, где C(0,1);

38.

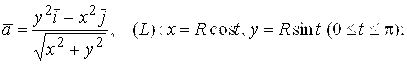
39. от точки (-1, 1) до точки (2, 2).

Вычислить линейный интеграл:

40.

41. , отрезок прямой от точки (1,1,1) до точки (4,4,4);

42.

43.

44. отрезок прямой от точки (0,0,0) до точки (1,1,1).

45. Дана напряженность силового поля. Найти работу поля при перемещении массы M вдоль одного витка винтовой линии , из точки в точку B (T =2p);

46. Силовое поле образовано силой, равной по величине расстоянию от начала координат до точки ее приложения и направленной к началу координат. Найти работу поля по перемещению единицы массы вдоль дуги параболы от точки с абсциссой до точки с абсциссой .

В задачах 47- 51 найти циркуляцию поля:

47. в отрицательном направлении;

48. Замкнутая линия, образованная отрезками осей координат Ox и Oy и другой астроиды , , лежащей в первом квадранте;

49.

50.

51. линия пересечения параболоида с координатными плоскостями (в первом октанте);

52. Твердое тело вращается с постоянной угловой скоростью вокруг оси Oz. Вычислить циркуляцию поля линейных скоростей вдоль окружности радиуса R, центр которой лежит на оси вращения, если плоскость окружности перпендикулярна оси вращения (циркуляция рассматривается в направлении вращения).

53. Найти работу поля при перемещении точки единичной массы вдоль замкнутой линии, состоящей из трех прямолинейных отрезков, лежащих в координатных плоскостях, отсекающих на осях координат отрезки, равные единице.

Найти дивергенцию нижеследующих полей:

54. . При какой функции будет ?

55. ; 56. - линейная скорость точек вращающейся жидкости - угловая скорость);

57. напряженность магнитного поля, J, – постоянные;

58. ; 59. ;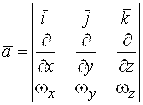

60. Вычислить в точке (1,-1,1).

Найти поток векторного поля через указанные замкнутые поверхности: 1) непосредственно, 2) по теореме Гаусса-Остроградского в векторной формулировке:

61.

62.

63.

64. ;

65.

66.

67.

68.

69.

70.

71.

72.

В задачах 73 и 74 вычислить ротор указанных векторных полей:

73. 74.

75. Показать, что если координаты вектора имеют непрерывные частные производные второго порядка, то .

76. Показать, что если и - постоянные векторы, то .

77. Показать, что .

78. Показать, что .

79. Показать, что векторное поле является безвихревым.

80. Показать, что ротор поля линейных скоростей точек вращающегося твердого тела есть постоянный вектор, направленный параллельно оси вращения, модуль которого равен удвоенной угловой скорости вращения: .