26. Криволинейные интегралы второго рода (КИ-2)

Пусть : 1) в точках непрерывной кривой AB из пространства определены ограниченные скалярные функции ;

2) - произвольное разбиение кривой AB на элементарные дуги С длинами и проекциями , , на соответствующие оси координат; 3) - произвольный набор точек;

4) 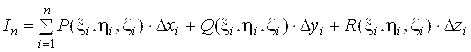- интегральная сумма, соответствующая данному разбиению и данному выбору точек.

Определение. Конечный предел интегральной суммы при , не зависящий ни от способа разбиения AB , ни от выбора точек , называется Криволинейным интегралом второго рода от функций По пути AB: .

Механически КИ-2 представляет собой Работу переменной силы , точка приложения которой описывает кривую AB.

Вычисление КИ-2. Теорема 14.7. Если линия AB задана в параметрической форме: , где - непрерывно дифференцируемые функции, и при изменении параметра T от К кривая описывается именно от точки A к точке B, то

(5.5)

Причем КИ-2 существует, если существует определенный интеграл.

Следствия.

А) Для плоской линии AB: И функций , : .

Б) Для заданной явно плоской линии

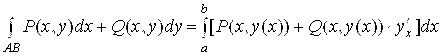. (5.6)

Независимость КИ-2 от пути интегрирования

Теорема 14.8. Если функции Непрерывны вместе со своими частными производными первого порядка в некоторой замкнутой ограниченной поверхностно односвязной области V, то равносильны следующие четыре утверждения:

1) , где L – замкнутый контур, лежащий внутри V;

2) не зависит от выбора пути интегрирования;

3) есть полный дифференциал некоторой однозначной функции , заданной в точках V;

4) выполняются равенства: .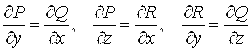

Функция Может быть найдена, например, по формуле

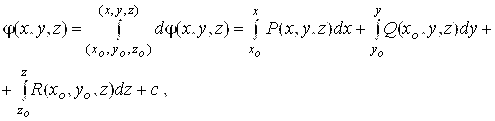(5.7)

Где - некоторая фиксированная точка области V, C – произвольная постоянная.

Связь между КИ-1 и КИ-2. Пусть спрямляемая (не имеющая особых точек) линия AB имеет в каждой точке касательную, положительное направление которой составляет с осью координат углы . Тогда

.

Связь КИ-2 с двойным интегралом (формула Грина). Теорема 14.9. Пусть: 1) функции непрерывны и имеют непрерывные частные производные в открытой односвязной области ; 2) L – кусочно-гладкий контур, ограничивающий область , и при положительном обходе L Ближайшая часть области S находится слева от наблюдателя. Тогда справедлива формула:

.

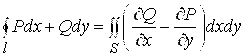Площадь плоской области. Площадь S фигуры S, ограниченной простым кусочно-гладким контуром L, равна

.

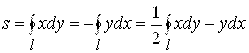Пример 20. Вычислить КИ-2: , где L – дуга параболы , проходимая от точки до точки .

Ñ Кривая L представлена на рис.14.24.

По формуле (5.6) имеем = =. #

Пример 21. Вычислить КИ-2: , где L – замкнутый контур, полученный пересечением сферы И цилиндра , обходимый против часовой стрелки, если смотреть из начала координат (рис.14.25).

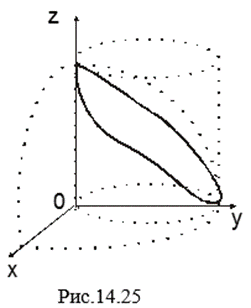
Ñ Для вычисления КИ-2 представим L в параметрической форме. Поверхность Запишем в виде .Последнее равенство выполнится тождественно, если положить, например, , , . Тогда из уравнения сферы имеем = = = =. Отсюда, помня, что , имеем . Итак, ; , , . По формуле (5.5) =

=.#

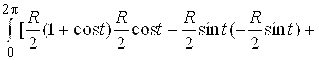
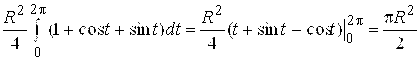Пример 22. Найти первообразную функции , если .

Ñ По формуле (5.7) при получим

.#

Задачи для самостоятельного решения

Вычислить криволинейные интегралы второго рода:

97. , где L – отрезок прямой от точки пересечения ее с осью Ox до точки пересечения с осью Oy.

98. , где L – контур прямоугольника с вершинами , указанными в порядке обхода L.

99. вдоль линий: 1) , 2) , 3) , 4) .

100. , L – эллипс , обходимый в положительном направлении.

101. , где L – первая от начала координат арки циклоиды , .

102. , где L – отрезок прямой от точки (1;1;1) до точки (2;3;4).

103. , где L – дуга винтовой линии .

104. , где L – линия пересечения сферы и цилиндра () , обходимая против часовой стрелки, если смотреть из начала координат (часть кривой Вивиани).

Убедиться, что подынтегральное выражение является полным дифференциалом, и вычислить КИ-2:

105. . 106. 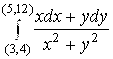. 107. .

108. (контурное интегрирование не пересекает поверхность .

Найти первообразную функцию и по полному дифференциалу:

109. .

110. .

111. .

112. .

113. 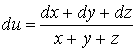. 114.

С помощью формулы Грина вычислить КИ-2:

115. , где L – окружность .

116. , где L – эллипс .

117. Вычислить , где L – простой замкнутый контур, пробегаемый в положительном направлении. Указание. Рассмотреть случаи: 1) начало координат находится вне контура L; 2) контур L окружает начало координат.

118. В каждой точке эллипса приложена сила , равная по величине расстоянию от точки M до центра эллипса и направленная к центру эллипса. Найти работу При перемещении в положительном направлении: а) вдоль дуги эллипса в первом октанте; б) вдоль всего эллипса.

119. Сила по величине обратно пропорциональна расстоянию точки ее приложения от оси Oz , перпендикулярна к этой оси и направлена к ней. Найти работу этой силы по окружности от точки до точки . Указание. .

< Предыдущая		Следующая >