23. Переход к сферическим координатам
Формулы ![]() ,
, ![]() ,
, ![]() преобразуют сферические координаты
преобразуют сферические координаты ![]() точки M в декартовы координаты этой точки и переводят область
точки M в декартовы координаты этой точки и переводят область ![]() (или
(или ![]()
![]()
![]() ) изменения сферических координат на все пространство Oxyz.
) изменения сферических координат на все пространство Oxyz.
Геометрически: R - радиус-ветор OM точки M; j - угол между осью Ox и проекцией радиус-вектора R на плоскость Oxy; y - угол между осью Oz и радиус-вектором R, отсчитываемый по ходу стрелки часов (рис.14.18).

Обратное преобразование имеет вид
![]() ,
, 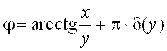 ,
,
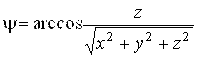 ,
, 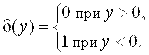
Фиксируя в последних формулах ![]() , получим тройку координатных поверхностей: сферу, полуплоскость, полуконус, соответственно (рис.14.18).Якобиан преобразования
, получим тройку координатных поверхностей: сферу, полуплоскость, полуконус, соответственно (рис.14.18).Якобиан преобразования
 .
.
При переходе в тройном интеграле к сферическим координатам справедлива формула:
![]() , (3.7)
, (3.7)
Где W - область изменения сферических координат точек области V из Oxyz.
Пример 12. Вычислить тройной интеграл ![]() , где
, где ![]() .
.
Ñ Область V ограничена полусферой ![]() и полуконусом
и полуконусом ![]() (рис.14.18). Для удобства вычисления тройного интеграла перейдем к сферическим координатам по формулам:
(рис.14.18). Для удобства вычисления тройного интеграла перейдем к сферическим координатам по формулам: ![]()
![]() , при этом
, при этом ![]() . Неравенства, описывающие V , преобразуются: а)
. Неравенства, описывающие V , преобразуются: а) ![]()
Б) ![]() .
.
Так как нет ограничений на ![]() , то
, то ![]() . В итоге, область интегрирования в сферических координатах есть
. В итоге, область интегрирования в сферических координатах есть 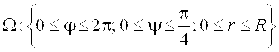 (этот же результат можно было усмотреть из чертежа). Тогда по формуле (3.7)
(этот же результат можно было усмотреть из чертежа). Тогда по формуле (3.7) ![]()
 =½повторный интеграл "расщепился" в произведение определенных интегралов ½=
=½повторный интеграл "расщепился" в произведение определенных интегралов ½=
=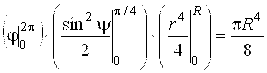 . #
. #
Пример 13. Вычислить тройной интеграл ![]() , где V ограничена полусферой
, где V ограничена полусферой ![]() , цилиндром
, цилиндром ![]() И плоскостью
И плоскостью ![]() .
.
Ñ Тело V и проекция его на плоскость Oxy ![]() - круг радиуса R изображены на рис.14.19 и 14.20. Для вычисления I перейдем к цилиндрическим координатам
- круг радиуса R изображены на рис.14.19 и 14.20. Для вычисления I перейдем к цилиндрическим координатам ![]() по формулам
по формулам ![]() . Поверхности, ограничивающие V преобразуются: а)
. Поверхности, ограничивающие V преобразуются: а) ![]() , б)
, б) ![]() , в) Z=A . Так как нет ограничений на координату
, в) Z=A . Так как нет ограничений на координату ![]() , то
, то ![]() (или
(или ![]() .Область интегрирования в цилиндрических координатах есть
.Область интегрирования в цилиндрических координатах есть ![]()
![]() .
.

Тогда по формуле (3.6) ![]() =
=![]() =
= 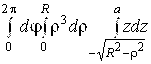 =
= =
= 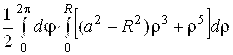 = =
= =![]() =
=![]() . #
. #
Задачи для самостоятельного решения
Перейти в тройном интеграле ![]() к цилиндрическим координатам
к цилиндрическим координатам ![]() или сферическим координатам
или сферическим координатам ![]() и расставить пределы интегрирования:
и расставить пределы интегрирования:
52. V – область, находящаяся в первом октанте и ограниченная поверхностями ![]() ,
, ![]() .
.
53. V – область, ограниченная поверхностями ![]() .
.
54. ![]() .
.
55. ![]() .
.
Перейдя к цилиндрическим или сферическим координатам, вычислить интегралы:
56.  . 57.
. 57.  .
.
58.  . 59.
. 59.  .
.
60. ![]() , где
, где ![]() .
.
61.  , где
, где ![]() .
.
62. 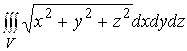 , где область V ограничена поверхностью
, где область V ограничена поверхностью ![]() .
.
| < Предыдущая | Следующая > |
|---|