22. Переход в тройном интеграле к цилиндрическим координатам

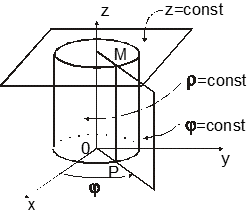
Формулы преобразуют цилиндрические координаты точки M в декартовы координаты этой точки и переводят область изменения криволинейных координат (или ) на все пространство Oxyz. Геометрически: r - радиус-вектор OM точки P – проекции точки M на плоскость Oxy; j - угол между Ox и OP; Z- аппликата точки M (рис. 14.17).

Обратное преобразование задается формулами:

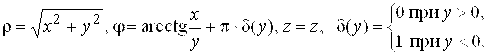
Фиксируя в последних формулах , получим тройку координатных поверхностей: круговой цилиндр с осью Oz , полуплоскость, исходящую из оси Oz, и плоскость, параллельную плоскости Oxy (рис.14.17).

Рис.14.17

Якобиан преобразования

При переходе в тройном интеграле к цилиндрическим координатам формула (3.5) примет вид0

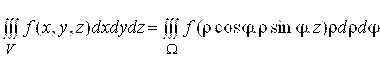, (3.6)

Где W - область изменения цилиндрических координат точек области V из Oxyz.

< Предыдущая		Следующая >