19. Тройные интегралы.. Области в пространстве

Определение. Область назовем Правильной в направлении Oz (Правильной в направлении Ox, Правильной в направлении Oy), если прямая, проходящая через внутреннюю точку области V параллельно оси Oz (параллельно оси Ox, параллельно оси Oy) пересекает границу области ровно в двух точках.

Область V будет Правильной в направлении Oz, если существуют функции и , заданные в S и такие, что координаты точек, принадлежащих V, удовлетворяют условиям: . Тогда символически записывают:

(3.1)

Если, в свою очередь, область S - правильная в направлении Oy, то (см.(2.1))

. (3.2)

Если область S правильная в направлении Ox, то (см.(2.2))

. (3.3)

Задания.

1. Записать символически правильную в направлении Oy область , если ее проекция на плоскость Oxz, в свою очередь, есть правильная область.

2. Записать символически правильную в направлении Ox область , если ее проекция на плоскость Oyz Есть правильная область.

Пример 10. Область V ограничена поверхностями и Z=0. Изобразить область и записать как правильную: а) в направлении Oz,

Б) в направлении Ox.

Ñ Область V - круговой конус с боковой поверхностью, описываемой уравнением конической поверхности , основанием, лежащим на плоскости Z=0, с вершиной в точке M(0;0;2) и осью, совпадающей с Oz (рис. 14.12).

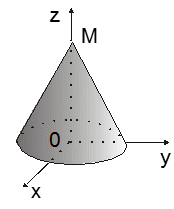
Область V - правильная во всех направлениях Ox, Oy, Oz. При Z=0 из уравнения имеем - уравнение окружности радиуса 2; таким образом, в основании конуса круг. а) Рассмотрим область V как правильную в направлении Oz. Из уравнения имеем . Для точек области V имеем: . Проекция области V на плоскость Oxy есть (рис. 14.13),

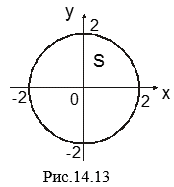
Поэтому в силу (3.1) ,где .Так как S - правильная область, то (см.(2.1)) или (см.(2.2)) . Поэтому требуемая запись будет (см. (3.2)) Или (см. (3.3)) .

Б) Рассматривая область V как правильную в направлении Ox, из уравнения имеем . Линии пересечения плоскости Oyz и конической поверхности находятся из решения системы уравнений: ; в результате имеем - прямые в плоскости Oyz. Итак, проекцией V на плоскость Oyz является область D - треугольник со сторонами Z=Y+2, Z = –Y+2, Z=0 (рис. 14.14),

Поэтому в силу (3.1) , где .

2

Так как область D – правильная, то рассматривая ее как правильную в направлении Oy, имеем , а потому

#

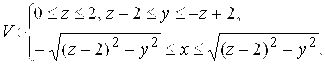Задачи для самостоятельного решения

Изобразить указанные ниже области И записать как правильные: а) в направлении Oz, б) в направлении Ox.

44. Область V Ограничена поверхностями .

45. Область V Ограничена поверхностями .

46. Область V Ограничена поверхностями .

< Предыдущая		Следующая >