18. Замена переменных в двойном интеграле
Пусть функции ![]() осуществляют взаимно однозначное непрерывно дифференцируемое отображение области P плоскости
осуществляют взаимно однозначное непрерывно дифференцируемое отображение области P плоскости ![]() на область S плоскости
на область S плоскости ![]() . Тогда существует обратное непрерывно дифференцируемое отображение
. Тогда существует обратное непрерывно дифференцируемое отображение ![]() ,
, ![]() области S на область P, если якобиан преобразования
области S на область P, если якобиан преобразования
 =
=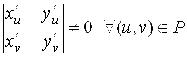 .
.
Величины U и V можно рассматривать как прямоугольные координаты для точек области P и в то же время как Криволинейные координаты точек области S. Точки плоскости Oxy, для которых одна из координат U и V сохраняет постоянное значение, образуют Координатную линию. Всего будет два семейства таких линий.
Теорема 14.3. Пусть ![]() есть дифференцируемое преобразование области P из плоскости
есть дифференцируемое преобразование области P из плоскости ![]() на область S Из плоскости
на область S Из плоскости ![]() . Тогда справедливо равенство
. Тогда справедливо равенство
![]() (2.5)
(2.5)
Замечание. Равенство (2.5) сохраняет справедливость, когда условие взаимно однозначного соответствия между областями S и P нарушается в отдельных точках или вдоль отдельных линий.
Переход в двойном интеграле к полярным координатам
Формулы
![]() (2.6)
(2.6)
Преобразуют полярные координаты ![]() точки в декартовы координаты этой точки и переводят область
точки в декартовы координаты этой точки и переводят область ![]() (или область
(или область ![]() ) на всю плоскость Oxy.
) на всю плоскость Oxy.
Обратное преобразование декартовых координат в полярные осуществляется по формулам: 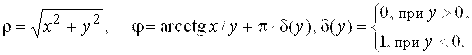
Фиксируя в последних формулах ![]() И
И![]() , получим координатные линии из разных семейств: окружность с центром в точке
, получим координатные линии из разных семейств: окружность с центром в точке ![]() И луч, исходящий из точки
И луч, исходящий из точки ![]() .
.
Якобиан преобразования

И формула (2.5) принимает вид:
![]() (2.7)
(2.7)
Рекомендация. К полярным координатам целесообразно переходить, когда в подынтегральное выражение или в уравнения границы области интегрирования входит комбинация ![]() .
.
В некоторых случаях при вычислении двойного интеграла удобно перейти от декартовых координат к Эллиптическим полярным Координатам ![]()
![]()
![]() по формулам
по формулам
![]() ,
, ![]() (2.8)
(2.8)
![]() - постоянные,
- постоянные, ![]() . Тогда
. Тогда
![]() ,
, ![]() (2.9)
(2.9)
Пример 6. Записать в полярной системе координат область S , заданную в декартовой системе координат неравенством ![]() (круг радиуса R с центром в точке
(круг радиуса R с центром в точке ![]() ).
).
Ñ Перейдем от декартовых координат X, Y к полярным ![]() по формулам
по формулам ![]() ,
, ![]() . Подставим X и Y в исходное неравенство, получим:
. Подставим X и Y в исходное неравенство, получим: ![]() или
или ![]() . На координату j дополнительных ограничений не накладывается, поэтому
. На координату j дополнительных ограничений не накладывается, поэтому ![]() (или
(или ![]() ).
).
В полярной системе координат круг записывается неравенствами: ![]() . #
. #
Пример 7. Записать в полярной системе координат область S - часть круга, ограниченную линиями ![]() ,
, ![]() ,
, ![]() (
(![]() ),
), ![]() - постоянные,
- постоянные, ![]() .
.
Ñ Изобразим область S (рис. 14.9). Запишем заданные линии в полярных координатах, которые связаны с декартовыми формулами ![]() ,
, ![]() : 1)
: 1)![]() Þ
Þ ![]() ;
;
2) ![]() Þ
Þ![]() ,
, ![]() ;
;
3)![]() Þ
Þ![]() .
.
Область ![]() переходит в область
переходит в область
![]() .
.
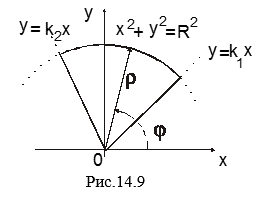
В полярной системе координат заданная область определяется системой неравенств: ![]() . #
. #
|
Пример 8. Вычислить двойной интеграл ![]() , S - множество точек, удовлетворяющих неравенству
, S - множество точек, удовлетворяющих неравенству ![]() .
.
Ñ Границей области является линия ![]() или
или ![]() - окружность радиуса 2 с центром в точке
- окружность радиуса 2 с центром в точке ![]() (Рис. 14.10).
(Рис. 14.10).
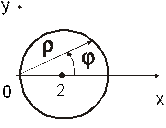
Рис. 14.10
Наличие в уравнении границы комбинации ![]() наводит на мысль, что для вычисления двойного интеграла удобно перейти к полярным координатам
наводит на мысль, что для вычисления двойного интеграла удобно перейти к полярным координатам ![]() по формулам
по формулам ![]() ,
, ![]() ,
, ![]() . Уравнение границы
. Уравнение границы ![]() переходит в уравнение
переходит в уравнение ![]() или
или ![]() . Отсюда r=0 (соответствует полюсу O) и
. Отсюда r=0 (соответствует полюсу O) и ![]() - уравнение окружности. Так как всегда
- уравнение окружности. Так как всегда ![]() (по смыслу r), то из
(по смыслу r), то из ![]() следует
следует ![]() , отсюда получаем
, отсюда получаем ![]() (этот же результат можно усмотреть из рисунка). Итак, в полярных координатах область интегрирования есть
(этот же результат можно усмотреть из рисунка). Итак, в полярных координатах область интегрирования есть 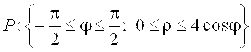 . Тогда по формуле (2.7)
. Тогда по формуле (2.7)
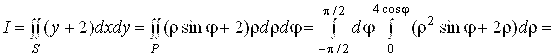


 . #
. #
Пример 9. Вычислить 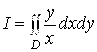 , где
, где ![]()
![]()
![]() .
.
Ñ Область D ограничена линиями: ![]() – эллипс с полуосями A и B,
– эллипс с полуосями A и B, ![]() – эллипс с полуосями
– эллипс с полуосями ![]() и
и ![]() , Y=0 – прямая (ось Ox),
, Y=0 – прямая (ось Ox), ![]() – прямая (рис. 14.11).
– прямая (рис. 14.11).
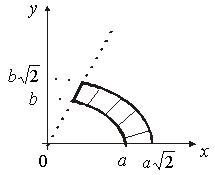
Рис.14.11
Анализ границы области указывает на целесообразность перехода к Эллиптическим полярным координатам по формулам (2.8), (2.9): ![]() ,
, ![]() . Уравнения границы области в координатах
. Уравнения границы области в координатах ![]() будут: 1)
будут: 1)![]() , 2)
, 2) ![]()
![]() , 3)
, 3) ![]() ,
,
4) ![]() . Итак, область интегрирования в координатах
. Итак, область интегрирования в координатах ![]() есть
есть
![]() . Тогда
. Тогда 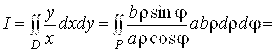
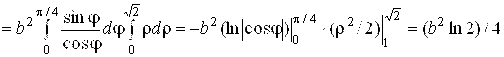 . #
. #
Задачи для самостоятельного решения
Перейти в двойном интеграле ![]() к полярным координатам
к полярным координатам ![]() и расставить пределы интегрирования в порядке: внешнее – по j, внутреннее - по r:
и расставить пределы интегрирования в порядке: внешнее – по j, внутреннее - по r:
27. D – область, ограниченная окружностями ![]() ,
, ![]() и прямыми
и прямыми ![]() ,
, ![]() .
.
28. D - область, являющаяся общей частью двух кругов ![]() и
и ![]() .
.
29. D - меньший из двух сегментов, на которые прямая ![]() рассекает круг
рассекает круг ![]() .
.
30. D - внутренняя часть правой петли лемнискаты Бернулли ![]() .
.
31. D:![]() .
.
32. D:  .Указание. Перейти к эллиптическим полярным координатам.
.Указание. Перейти к эллиптическим полярным координатам.
33. D - область, ограниченная линией ![]() . Указание. Перейти к эллиптическим полярным координатам.
. Указание. Перейти к эллиптическим полярным координатам.
34. 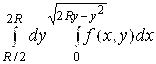 . 35.
. 35.  . 36.
. 36. 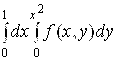 .
.
С помощью перехода к полярным координатам вычислить интегралы:
37.  . 38.
. 38. ![]() .
.
39.  . 40.
. 40. 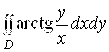 , D - часть кольца
, D - часть кольца ![]() ,
,
![]() ,
, ![]() . 41.
. 41. 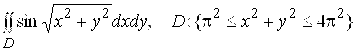 .
.
Вычислить, перейдя к эллиптическим полярным координатам, интегралы:
42.  .
.
43. ![]() - область, ограниченная линией
- область, ограниченная линией ![]() .
.
| < Предыдущая | Следующая > |
|---|