17. Вычисление двойного интеграла в декартовых координатах
Теорема 14.1 Если : 1) функция F(X,Y) интегрируема в правильной в направлении Oy области S: ![]() , т. е. существует двойной интеграл
, т. е. существует двойной интеграл ![]() , 2) существует повторный интеграл
, 2) существует повторный интеграл 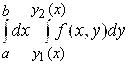 , то
, то
 (2.3)
(2.3)
Теорема 14.2. Если :1) функция F(X,Y) интегрируема в правильной в направлении Ox области ![]() , т. е. существует двойной интеграл
, т. е. существует двойной интеграл ![]() , 2) существует повторный интеграл
, 2) существует повторный интеграл 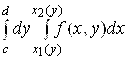 , то
, то
 . (2.4)
. (2.4)
Из вышеприведенных теорем следует, что При вычислении повторного интеграла можно изменять порядок интегрирования.
Пример 4. Изменить порядок интегрирования в интеграле 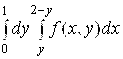 .
.
|
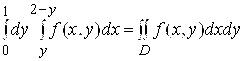 , то правильная в направлении Ox область D ограничена линиями X=Y, X=2-Y, Y=0, Y=1 (линия Y =1 выродилась в точку) (рис. 14.7). Эта область является правильной и в направлении Oy. Так как участок OAB Границы состоит из отрезков прямых
, то правильная в направлении Ox область D ограничена линиями X=Y, X=2-Y, Y=0, Y=1 (линия Y =1 выродилась в точку) (рис. 14.7). Эта область является правильной и в направлении Oy. Так как участок OAB Границы состоит из отрезков прямых 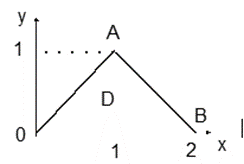
![]() . Итак,
. Итак, 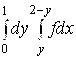 =
= ![]() =
= ![]() =
=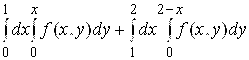 .#
.#
Пример 5. Вычислить ![]() по области D, ограниченной линиями
по области D, ограниченной линиями ![]() и
и ![]() .
.
Ñ Изобразим область D. Для отыскания точек пересечения парабол ![]() и
и ![]() решаем уравнение
решаем уравнение ![]()
![]() , откуда имеем действительные корни
, откуда имеем действительные корни ![]() ,
, ![]() . Таким образом, параболы пересекаются в точках
. Таким образом, параболы пересекаются в точках ![]() ( рис. 14.8). Рассматривая D как правильную в направлении Oy (рис.14.8а), имеем (см.(2.1))
( рис. 14.8). Рассматривая D как правильную в направлении Oy (рис.14.8а), имеем (см.(2.1)) ![]() . По формуле (2.3)
. По формуле (2.3)
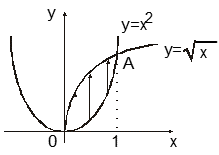
Рис.14.8 а)

=
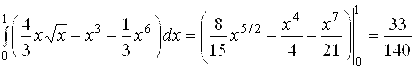 .
.
Если область D рассматривать как правильную в направлении Ox (рис.14.8б), 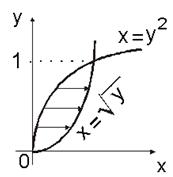
Рис.14.8.б
То (см. (2.2)) ![]() . По формуле (2.4)
. По формуле (2.4)
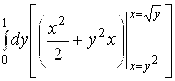 =
=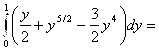
|
|
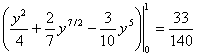 . #
. #
Задачи для самостоятельного решения
Изменить порядок интегрирования в следующих повторных интегралах:
8. 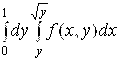 . 9.
. 9. 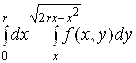 .
.
10. 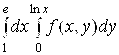 . 11.
. 11.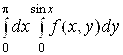 .
.
Перейти от двойного интеграла ![]() по конечной области D к повторному интегралу и расставить пределы интегрирования:
по конечной области D к повторному интегралу и расставить пределы интегрирования:
12. Область D – параллелограмм со сторонами ![]()
![]()
![]() .
.
13. ![]() . 14.
. 14. ![]() .
.
15. ![]() - треугольник со сторонами
- треугольник со сторонами ![]() .
.
16. ![]() .
.
17. ![]() - треугольник с вершинами
- треугольник с вершинами ![]() .
.
18. D – сегмент, ограниченный линиями ![]() .
.
Вычислить двойные интегралы:
19. ![]() . 20.
. 20. ![]() - Круг
- Круг ![]() .
.
21. ![]() - область, ограниченная линиями
- область, ограниченная линиями ![]() .
.
22.  - область, ограниченная линиями
- область, ограниченная линиями ![]() .
.
23. ![]() - область, ограниченная линиями
- область, ограниченная линиями ![]() .
.
24.![]() - четверть круга
- четверть круга ![]() , лежащая в первом квадранте.
, лежащая в первом квадранте.
25. ![]() - область, ограниченная параболой
- область, ограниченная параболой ![]() и прямой
и прямой ![]() .
.
26. ![]() , если D ограничена осью абсцисс и первой аркой циклоиды
, если D ограничена осью абсцисс и первой аркой циклоиды ![]() ,
, ![]() ,
, ![]() .
.
| < Предыдущая | Следующая > |
|---|