20. Вычисление тройного интеграла в декартовых координатах
Пусть правильная в направлении Oz область V ограничена снизу и сверху непересекающимися поверхностями ![]() и
и ![]() , а с боков – цилиндрической поверхностью F(X,Y)=0 c образующими, параллельными оси Oz, т. е.
, а с боков – цилиндрической поверхностью F(X,Y)=0 c образующими, параллельными оси Oz, т. е.
![]() , где S- проекция V на плоскости Oxy.
, где S- проекция V на плоскости Oxy.
Теорема 14.4. Пусть:1) в области ![]() Задана функция F(X,Y,Z), интегрируемая по Риману, т. е. существует тройной интеграл
Задана функция F(X,Y,Z), интегрируемая по Риману, т. е. существует тройной интеграл ![]() ; 2) существует повторный интеграл
; 2) существует повторный интеграл  . Тогда справедлива формула
. Тогда справедлива формула
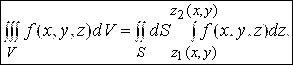 (3.4)
(3.4)
Замечание. Цилиндрическая поверхность ![]() , ограничивающая V, может частично или полностью вырождаться в пространственную линию.
, ограничивающая V, может частично или полностью вырождаться в пространственную линию.
Задания. Записать формулы, связывающие тройной интеграл с повторным, в случаях, когда: 1) область V правильная в направлении Ox проецируется на плоскость Oyz; 2) область V правильная в направлении Oy проецируется на плоскость Oxz.
Пример 11. Вычислить ![]() , где область V ограничена
, где область V ограничена
Поверхностями: ![]() .
.
Ñ Поверхности ![]() И
И ![]() есть параболические цилиндры с образующими, параллельными
есть параболические цилиндры с образующими, параллельными ![]() - плоскости. Область V – правильная в направле-
- плоскости. Область V – правильная в направле-
Нии Oz, а потому ![]() для точек, принадлежащих V (рис.14.15).
для точек, принадлежащих V (рис.14.15).

Проекция V на плоскость Oxy есть правильная область S, ограниченная линиями ![]() и
и ![]() ,а потому, например (см.(2.1)),
,а потому, например (см.(2.1)), ![]() и в силу (3.2)
и в силу (3.2) ![]() . Тогда по формуле (3.4)
. Тогда по формуле (3.4) ![]() =
= 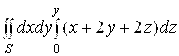 =
=
= =½см. (2.3)½=
=½см. (2.3)½=  =
= =
=![]() #
#
Задачи для самостоятельного решения
Вычислить интегралы:
47.  .
.
48.  , W - область, ограниченная плоскостями
, W - область, ограниченная плоскостями ![]() ,
,
![]() .
.
49. ![]() , V – область, ограниченная гиперболическим параболоидом
, V – область, ограниченная гиперболическим параболоидом ![]() и плоскостями
и плоскостями ![]() .
.
50. ![]()
![]() , V – область, ограниченная цилиндром
, V – область, ограниченная цилиндром ![]() и плоскостями
и плоскостями ![]() и
и ![]() .
.
51. ![]() , V – область, ограниченная поверхностями
, V – область, ограниченная поверхностями ![]()
![]()
![]() .
.
| < Предыдущая | Следующая > |
|---|