14. Кратные интегралы. Определение кратного интеграла. Определение двойного и тройного интеграла

Пусть : 1) в ограниченной замкнутой области “ объема” v(E) задана ограниченная функция ; 2) - разбиение области на подобласти с объемами 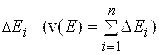И диаметрами , - диаметр разбиения; 3) зафиксируем точки , ; 4) построим Интегральную сумму

.

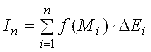Определение. Конечный предел I интегральной суммы при называется M- Кратным Интегралом от функции F по области E и обозначается

Или . (1.1)

Таким образом, по определению,

(1.2)

В этом случае функция называется Интегрируемой в E.

При M=2 (M=3) для ограниченной функции F в замкнутой области ) кратный интеграл (1.1) называется Двойным (Тройным) Интегралом, а соответствующее определение (1.2) примет вид

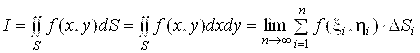,где точка (,

Где точка .

< Предыдущая		Следующая >