10. Экстремум функции 2-х переменных

Пусть - внутренняя точка области определения функции . Точка называется точкой Минимума (Максимума) функции F, если существует такая окрестность точки , что для любой точки выполняется .

Точка называется точкой Экстремума функции F, если она является точкой минимума или точкой максимума этой функции.

Теорема 9.7. (Необходимое условие экстремума.) Если - точка экстремума функции, то каждая частная производная и либо равна нулю, либо не существует.

Точка называется Критической точкой функции F, если в ней выполняются необходимые условия экстремума функции F.

Теорема 9.8. (Достаточные условия экстремума.) Пусть: а) - критическая точка функции F, б) существуют и непрерывны производные в точках и , в) .Тогда: 1) если и , то - точка минимума функции F ; 2) если и , то - точка максимума функции F ; 3) если , то Не является точкой экстремума; 4) если , то требуется дополнительное исследование.
Отметим, что в случае существуют такие две прямые, проходящие через точку , что при движении точки M по первой из этих прямых значения функции сначала уменьшаются, затем возрастают. При движении точки М по другой прямой значения функции сначала возрастают, в точке Достигают максимума, затем уменьшаются. В этом случае точку называют седловой.

Пример 16. Исследовать на экстремум функцию .

Ñ Из необходимого условия экстремума функции (теорема 9.7) имеем систему 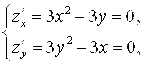решая которую получаем критические точки . Определим характер критических точек по достаточным условиям экстремума. Находим . В точке : , , , . Следовательно, - седловая точка. В точке : , , , поэтому - точка минимума функции z; . #

< Предыдущая		Следующая >