08. Приложения частных производных и дифференциала. Приложение дифференциала к приближенным вычислениям
Для дифференцируемой функции 
при достаточно малом
Из формул (5.1) – (5.3) следует
Или, что то же самое,
. (7.1)
Пример 14. Вычислить приближенно 
.
Ñ Искомое число будем рассматривать как значение функции 
при 
и 
, если 
. Точка 
выбрана из соображений близости ее к точке 
и простоты вычисления значений функции F И ее частных производных в точке М. По формуле (7.1) имеем 
.
Находим 
, 
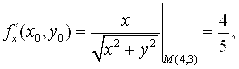
. Следовательно, 
»
. #
| < Предыдущая | Следующая > |
|---|
