07. Неявные функции одной и нескольких независимых
Переменных
1°. Пусть дифференцируемая в точке X0 функция Y(X) задана неявно уравнением ![]() и Y=Y(X) - решение этого уравнения. Если функция F дифференцируема, то производная функции Y=Y(X) определяется формулой
и Y=Y(X) - решение этого уравнения. Если функция F дифференцируема, то производная функции Y=Y(X) определяется формулой
 (6.4)
(6.4)
При условии, что ![]() , где Y0 = Y (X0), F (X0,Y0) = 0.
, где Y0 = Y (X0), F (X0,Y0) = 0.
2°. Пусть дифференцируемая в точке ![]() функция
функция ![]() задана неявно уравнением
задана неявно уравнением ![]() и U =
и U =![]() - решение этого уравнения.
- решение этого уравнения.
Если F Дифференцируема, то частные производные функции U =![]() в точке М 0 определяются по формулам
в точке М 0 определяются по формулам
 (6.5)
(6.5)
При условии, что ![]() , где
, где ![]() .
.
Пример 12. Найти ![]() , если
, если ![]() .
.
Ñ ![]() и по формуле (6.4) получаем
и по формуле (6.4) получаем  =
= . В нашем случае X0 = 0. Непосредственной подстановкой убедимся, что точка
. В нашем случае X0 = 0. Непосредственной подстановкой убедимся, что точка ![]() принадлежит графику функции, т. е.
принадлежит графику функции, т. е. ![]() . Поэтому
. Поэтому 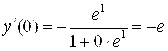 .#
.#
Пример 13. Найти 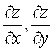 , если
, если ![]() .
.
ÑЛевую часть данного уравнения обозначим ![]() . По формуле (6.5) получим:
. По формуле (6.5) получим: ,
,  .#
.#
Задачи для самостоятельного решения
37. Найти ![]() , если
, если ![]() где
где ![]() ,
, ![]() .
.
38. Найти ![]() , если
, если ![]() , где X = ln T, Y = sin T.
, где X = ln T, Y = sin T.
39. Найти ![]() , если
, если ![]() где
где ![]() .
.
40. Найти ![]() и
и ![]() , если
, если ![]() , где
, где ![]() .
.
41. Найти ![]() и
и ![]() , если
, если 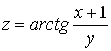 , где
, где ![]() .
.
42. Найти ![]() , если
, если ![]() , где
, где ![]() .
.
43. Найти Dz, если ![]() , где
, где ![]() .
.
44. Найти ![]() , если
, если ![]() , где
, где ![]() .
.
45. Найти Dz, если ![]() , где
, где ![]() .
.
46. Найти ![]() , если: а)
, если: а) ![]() , б)
, б) ![]() .
.
47. Найти 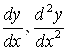 , если: а)
, если: а) ![]() , б)
, б) ![]() .
.
48. Найти ![]() и
и ![]() в точке (1,-2,2), если
в точке (1,-2,2), если ![]() .
.
49. Найти ![]() и
и ![]() , если: а)
, если: а) ![]() , б)
, б) ![]() .
.
Рекомендация. Ввести ![]() .
.
| < Предыдущая | Следующая > |
|---|