06. Дифференцирование сложных и неявных функций. Сложные функции одной и нескольких переменных
1°. Пусть ![]() и в свою очередь,
и в свою очередь, ![]() .
.
Теорема 9.5. Если функции ![]() дифференцируемы в точке
дифференцируемы в точке ![]() , то для производной сложной функции одной переменной
, то для производной сложной функции одной переменной ![]() справедлива формула
справедлива формула
![]() или
или
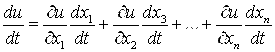 . (6.1)
. (6.1)
В частности, если T Совпадает, например, с переменной ![]() , то
, то ![]() и “полная” производная функции И По
и “полная” производная функции И По ![]() равна
равна
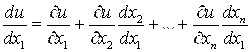 . (6.2)
. (6.2)
2°. Пусть ![]() и, в свою очередь,
и, в свою очередь, ![]() ,
, ![]() .
.
Теорема 9.6. Если функции ![]() дифференцируемы в точке
дифференцируемы в точке ![]() , а функция F дифференцируема в точке
, а функция F дифференцируема в точке ![]() , то сложная функция M переменных
, то сложная функция M переменных ![]() дифференцируема в точке N и справедливы формулы:
дифференцируема в точке N и справедливы формулы:
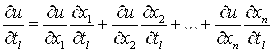
![]() , (6.3)
, (6.3)
При этом частные производные функции U по ![]() вычислены в точке М, а частные производные функций
вычислены в точке М, а частные производные функций ![]() По
По ![]() (L=1,2,…,M) вычислены в точке N.
(L=1,2,…,M) вычислены в точке N.
Выражение для дифференциала 1-го порядка сохраняет вид (5.4) (Свойство инвариантности формы первого дифференциала).
Пример 8. Найти ![]() , если
, если ![]() , где
, где ![]() .
.
Ñ По формуле (6.1) имеем 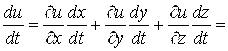
![]()
![]()
![]() . #
. #
Пример 9. Найти производную функции ![]() .
.
Ñ Первый способ – применить логарифмическое дифференцирование, как делалось для функции одной переменной.
Второй способ. Функция U(T) есть результат образования сложной функции при подстановке в функцию ![]() вместо X и Y двух одинаковых функций переменой T:
вместо X и Y двух одинаковых функций переменой T: ![]()
![]() . Тогда по формуле (6.1):
. Тогда по формуле (6.1): ![]() +
+![]() получаем
получаем ![]() =
=![]()
![]()
+![]()
![]() .#
.#
Пример 10. Найти ![]() и
и ![]() , если
, если ![]() , где Y = sin2X.
, где Y = sin2X.
Ñ Имеем ![]() . По формуле (6.2) получим
. По формуле (6.2) получим 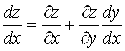 =
= ![]() .#
.#
Пример 11. Найти 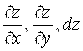 , если
, если ![]() , где
, где ![]() ,
, ![]() .
.
Ñ ![]() - сложная функция от независимых переменных x и y. Тогда по формулам (6.3) получим:
- сложная функция от независимых переменных x и y. Тогда по формулам (6.3) получим: 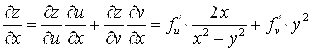 ;
;
 ;
; ![]() ,
,
 ,
, ![]() ,
,
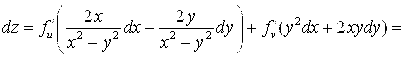
![]()
 .#
.#
| < Предыдущая | Следующая > |
|---|