05. Дифференцируемость функции. Дифференциал функции

1°. Полным приращением функции в точке , соответствующим приращениям аргументов , называется разность
. (5.1)

2°.Функция F называется Дифференцируемой В точке М, если существуют такие числа , что всюду в окрестности точки М полное приращение

Функции можно представить в виде

Где .

Теорема 9.3 (Необходимое условие дифференцируемости функции.) Если функция F дифференцируема во внутренней точке , то существуют частные производные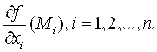

Теорема 9.4. (Достаточное условие дифференцируемости функции). Если частные производные 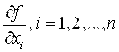существуют и непрерывны во внутренней точке , то функция дифференцируема в М. Для дифференцируемой в точке М функции F полное приращение
(5.2)

3°. Дифференциалом Df первого порядка функции в точке называется главная часть полного приращения (5.2), линейная относительно :

. (5.3)

Подставив в (5.2) , получим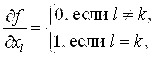

L = 1,2,…,N и или . Тогда дифференциал функции F Выражается через дифференциалы независимых переменных:

. (5.4)

Функции U и V нескольких переменных подчиняются обычным правилам дифференцирования:

, , . (5.5)

4°.Дифференциалом 2-го порядка функции называется дифференциал от ее дифференциала 1-го порядка, рассматриваемого как функция переменных при фиксированных (т. е. постоянных) :

. Вообще, Дифференциал M – го порядка функции F:

(5.6)

Пример 5. Найти полное приращение и дифференциал функции в точке .

Ñ По формуле (5.1) =.

Дифференциал Df есть главная часть полного приращения, линейная относительно : .#

Пример 6. Найти дифференциал функции .

Первый способ. По формуле (5.4): ,

Второй способ. Применяем правила дифференцирования (5.5):

. #

Пример 7. Найти дифференциалы 1-го, 2-го и 3-го порядков для функции .

Ñ По формуле (5.4): . По формуле (5.6) при M = 2 и M = 3, считая Dx и Dy постоянными, последовательно находим (смешанные частные производные не зависят от порядка дифференцирования):