04. Частные производные и дифференцируемость функции
1°. Пусть M(X1,…,Xk,…,Xn) – произвольная фиксированная точка из области определения D функции ![]() и точка
и точка ![]() Если существует предел
Если существует предел
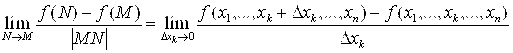 ,
,
То он называется Частной производной первого порядка данной функции по переменной Xk в точке M и обозначается ![]() или
или ![]() , или
, или ![]() .
.
Частные производные вычисляются по правилам дифференцирования функции одной переменной, при этом все переменные, кроме Xk , рассматриваются как постоянные.
2°. Частными производными второго порядка функции ![]() по соответствующим переменным называются частные производные от ее частных производных первого порядка, они обозначаются:
по соответствующим переменным называются частные производные от ее частных производных первого порядка, они обозначаются: ![]()
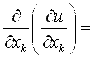 =
=![]() ,
, 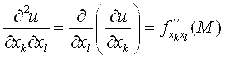 и т. д. Аналогично определяются частные производные порядка выше второго.
и т. д. Аналогично определяются частные производные порядка выше второго.
Теорема 9.2 Если смешанные производные ![]() Непрерывны, то они совпадают:
Непрерывны, то они совпадают: ![]() .
.
Таким образом, результат многократного дифференцирования функции по различным переменным не зависит от порядка дифференцирования при условии, что возникающие при этом “смешанные” частные производные непрерывны.
Пример 4. Найти частные производные первого и второго порядков от функции ![]() .
.
Ñ Считая последовательно постоянной “Y”, затем “X”, и применяя правило дифференцирования сложной функции, получим: 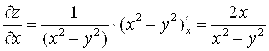 ,
,
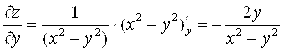 . Дифференцируя вторично, получим:
. Дифференцируя вторично, получим:
 ,
,
 ,
,
 ,
,
 .#
.#
Задачи для самостоятельного решения
Найти частные производные 1-го и 2-го порядков от заданных функций:
20. ![]() . 21.
. 21. ![]() . 22.
. 22. ![]() . 23.
. 23. ![]() .
.
24. ![]() . 25. Найти
. 25. Найти ![]() , если
, если ![]() .
.
| < Предыдущая | Следующая > |
|---|