02. Предел функции
Пусть функция ![]() определена на множестве D И точка
определена на множестве D И точка ![]() .
.
1°. Число А называется Пределом Функции F(M) при стремлении точки ![]() к точке
к точке ![]() (или, другими словами, при
(или, другими словами, при ![]() , если для любого, сколь угодно малого положительного e найдется такая d - окрестность точки
, если для любого, сколь угодно малого положительного e найдется такая d - окрестность точки ![]() , что для любой точки M из этой окрестности выполняется
, что для любой точки M из этой окрестности выполняется ![]() и обозначается
и обозначается ![]()
![]() . Этот предел Не должен зависеть От способа (“пути”) стремления M к М0.
. Этот предел Не должен зависеть От способа (“пути”) стремления M к М0.
Используя логические символы ![]()
![]()
![]()
![]() .Для функции двух переменных F (X,Y)
.Для функции двух переменных F (X,Y) 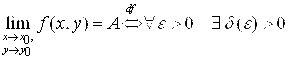
![]()
![]()
![]() .
.
2°. Функция F(M) называется Бесконечно малой функцией (б. м.ф.) при стремлении M к точке M0, если ![]()
![]()
![]()
![]()
![]() . Практически, при вычислении
. Практически, при вычислении ![]() удобно задать проходящую через точки M и М0 линию в параметрической (или иной ) форме, сведя тем самым задачу к вычислению предела функции одной переменной по известным правилам и теоремам.
удобно задать проходящую через точки M и М0 линию в параметрической (или иной ) форме, сведя тем самым задачу к вычислению предела функции одной переменной по известным правилам и теоремам.
Пример 2. Вычислить пределы: а) 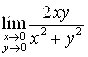 , б)
, б) ![]()
Ñ а) Пусть точка M(X,Y) из окрестности точки M0(0,0) стремится к точке М0 по прямой Y=Kx ( проходящей через точки М0 и М). Тогда из ![]() следует
следует ![]() и
и 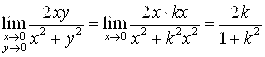 . Пределы получаются разными при различных “K” и не существует числа A, к которому значения
. Пределы получаются разными при различных “K” и не существует числа A, к которому значения 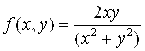 становились бы сколь угодно близки, как только точка M(X,Y) оказывается в достаточной близости от точки M0(0,0). Предел данной функции при M®M0(0,0) не существует.
становились бы сколь угодно близки, как только точка M(X,Y) оказывается в достаточной близости от точки M0(0,0). Предел данной функции при M®M0(0,0) не существует.
Б) ![]() =½находим предел вдоль луча Y=Kx (K>0,
=½находим предел вдоль луча Y=Kx (K>0, ![]() ) при X®¥½=
) при X®¥½= ½применим правило Лопиталя два раза½=
½применим правило Лопиталя два раза½=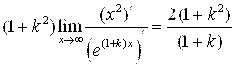 .
. 
 – предел существует и равен нулю. #
– предел существует и равен нулю. #
Задачи для самостоятельного решения
Вычислить пределы функций, полагая, что независимые переменные произвольно стремятся к своим предельным значениям.
9. 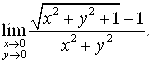 10.
10. 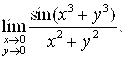 11.
11. 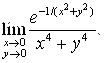
12. 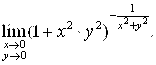 13.
13. 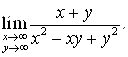
| < Предыдущая | Следующая > |
|---|