01. Функции нескольких переменных. Основные понятия и определения
1°.![]() - множество всех упорядоченных пар чисел (X,Y) (троек чисел (X,Y,Z)).
- множество всех упорядоченных пар чисел (X,Y) (троек чисел (X,Y,Z)). ![]() - множество всех упорядоченных наборов N Чисел
- множество всех упорядоченных наборов N Чисел ![]() .
.
2°. Функция F N переменных сопоставляет по определенному правилу каждому набору N чисел ![]() из Области определения
из Области определения ![]() единственное значение U из Области значений
единственное значение U из Области значений ![]() , что записывается в виде
, что записывается в виде ![]() или
или ![]() В дальнейшем будем рассматривать функции двух (трех) переменных
В дальнейшем будем рассматривать функции двух (трех) переменных ![]() ,
, ![]()
![]() .
.
3°. Если (X,Y) (или (X,Y,Z)) - декартовы координаты точки плоскости Oxy (или пространства Oxyz), то D – часть плоскости или вся плоскость (часть пространства или все пространство).
4°.E - окрестность точки ![]() - множество всех точек
- множество всех точек ![]() , не совпадающих с точкой
, не совпадающих с точкой ![]() , расстояние до которых от точки
, расстояние до которых от точки ![]() меньше e:
меньше e: ![]() . Так, e - окрестность точки
. Так, e - окрестность точки ![]() - множество точек M(X,Y), удовлетворяющих условию
- множество точек M(X,Y), удовлетворяющих условию ![]() - шар радиуса e без границы с выколотым центром
- шар радиуса e без границы с выколотым центром ![]() .
.
5°. Назовем точку Внутренней точкой области, если она принадлежит этой области вместе со всеми точками какой – нибудь своей окрестности. Любая окрестность Граничной точки области содержит точки, принадлежащие области, и точки, не принадлежащие области. Сами граничные точки могут принадлежать области, а могут не принадлежать.
6°. Область называется Замкнутой, если она содержит все свои граничные точки.
Пример 1. Найти и изобразить область определения функций:
а) ![]() ; б)
; б) ![]() .
.
Ñ а) функция определена, если X и Y удовлетворяют системе неравенств (которую последовательно решаем)

 Следовательно, область определения множество точек
Следовательно, область определения множество точек ![]()
![]() .Область определения изображена на рис. 9.1.
.Область определения изображена на рис. 9.1.
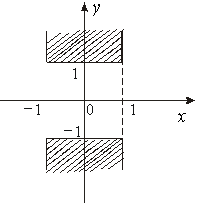 Б) функция определена, если X и Y Удовлетворяют системе неравенств
Б) функция определена, если X и Y Удовлетворяют системе неравенств
|

Область определения получается пересечением множеств: ![]() - множество точек “под” параболой
- множество точек “под” параболой ![]() , включая саму параболу;
, включая саму параболу; ![]() - внутренность круга радиуса 1 с центром в точке
- внутренность круга радиуса 1 с центром в точке ![]() ,
, ![]() - вся плоскость Oxy, исключая точку
- вся плоскость Oxy, исключая точку
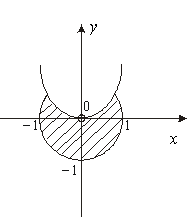
![]() . Итак,
. Итак, ![]()
![]()
![]() (рис. 9.2).
(рис. 9.2).
|
Задачи для самостоятельного решения
Найти области определения следующих функций:
1. ![]() . 2.
. 2. ![]() . 3.
. 3. ![]() .
.
4. ![]() . 5.
. 5. ![]() . 6.
. 6. ![]() . 7.
. 7. ![]() . 8.
. 8. ![]()
| Следующая > |
|---|