7.6. Обобщённые функции
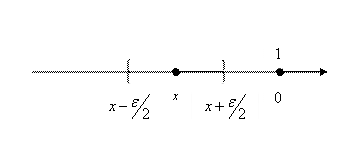
Рассмотрим ось ![]() и будем полагать, что в точке
и будем полагать, что в точке ![]() Находится масса равная 1. Вычислим линейную плотность некоторого отрезка, лежащего на оси
Находится масса равная 1. Вычислим линейную плотность некоторого отрезка, лежащего на оси ![]() . Линейная плотность выражается, как предел:
. Линейная плотность выражается, как предел: ![]() , где
, где ![]() – масса сегмента длины
– масса сегмента длины ![]() . Пусть линейная плотность обозначается
. Пусть линейная плотность обозначается ![]() , тогда если
, тогда если ![]() , если
, если ![]() . Итак:
. Итак: ![]() . Функция
. Функция ![]() описывает линейную плотность. Попробуем из плотности получить массу, тогда:
описывает линейную плотность. Попробуем из плотности получить массу, тогда: 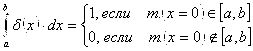 . В точности, условие нормировки:
. В точности, условие нормировки:
![]()
Но интегрируема ли эта функция? «Размажем» единичную массу по отрезку ![]() , тогда:
, тогда:  При
При ![]() поточечный предел
поточечный предел ![]() :
: ![]() . Поточечный предел функции
. Поточечный предел функции ![]() по сегменту
по сегменту ![]() равен 1.
равен 1.
Другой подход: Пусть ![]() – произвольная непрерывная функция, заданная на всей числовой прямой. Докажем, что
– произвольная непрерывная функция, заданная на всей числовой прямой. Докажем, что
![]()
Т. е. нужно доказать, что  .
.
Док-во:  ;
; ![]() – непрерывна в точке
– непрерывна в точке ![]()
 , ч. т.д.
, ч. т.д.
Обозначение: ![]() . Тогда формула (1) принимает вид:
. Тогда формула (1) принимает вид: ![]() .
.

В частности: ![]() , тем самым выполняется (1).
, тем самым выполняется (1).
Определение: Обобщённая ![]() -функция (
-функция (![]() -функция Дирака) – это такая функция, что для любой непрерывной функции
-функция Дирака) – это такая функция, что для любой непрерывной функции ![]() :
: ![]() .
.
Таким образом ![]() -функция ставит в соответствие любой непрерывной функции
-функция ставит в соответствие любой непрерывной функции ![]() её значение
её значение ![]() . Если каждой функции из некоторого множества поставить в соответствие некоторое число, то говорят, что на данном множестве задан функционал. Введённая
. Если каждой функции из некоторого множества поставить в соответствие некоторое число, то говорят, что на данном множестве задан функционал. Введённая ![]() -функция представляет собой функционал, заданный на множестве непрерывных функций. Будем рассматривать функции
-функция представляет собой функционал, заданный на множестве непрерывных функций. Будем рассматривать функции ![]() , заданные на всей числовой прямой от
, заданные на всей числовой прямой от ![]() до
до ![]() , обладающими следующими свойствами: 1)
, обладающими следующими свойствами: 1) ![]() – бесконечно дифференцируемая функция, 2)
– бесконечно дифференцируемая функция, 2) ![]() – финитная функция, т. е. равна 0 вне некоторого интервала (для любой функции
– финитная функция, т. е. равна 0 вне некоторого интервала (для любой функции ![]() свой интервал).
свой интервал).
Пусть ![]() – множество, на котором указанные функции
– множество, на котором указанные функции ![]() не равны нулю.
не равны нулю. ![]() – замкнутые множества
– замкнутые множества ![]() , т. е.
, т. е. ![]() все предельные точки, D – множество основных функций.
все предельные точки, D – множество основных функций.
Определение: Множество финитных бесконечно дифференцируемых функций назовём множеством основных функций и обозначим их как D.
Определение: Будем говорить, что последовательность ![]() основных функций сходится к функции
основных функций сходится к функции ![]() из множества
из множества ![]() , если:
, если:
1. ![]()
2. ![]() , где
, где ![]() – натуральное
– натуральное ![]() на
на ![]() .
.
Обозначение: ![]() при
при ![]() в D.
в D.
Множество D основных функций с введённой в нём сходимостью называется пространством основных функций, которое также обозначается буквой D.
Определение: Говорят, что на пространстве D задан функционал, если каждой функции ![]() поставлено в соответствие некоторое число
поставлено в соответствие некоторое число ![]() .
.
Определение: Функционал ![]() называется линейным, если
называется линейным, если ![]()
![]() .
.
Определение: Функционал F, определённый на пространстве D основных функций, называется непрерывным, если для любой последовательности имеем: ![]() .
.
Определение: Обобщённой функцией называется всякий линейный непрерывный функционал, определённый на пространстве основных функций.
Определим сумму двух обобщённых функций ![]() и
и ![]() , как обобщённую функцию, действующую по формуле:
, как обобщённую функцию, действующую по формуле: ![]() , а произведение обобщённой функции
, а произведение обобщённой функции ![]() на число
на число ![]() , как обобщённую функцию действующую по формулу:
, как обобщённую функцию действующую по формулу: ![]() . Нетрудно доказать, что
. Нетрудно доказать, что ![]() и
и ![]() - линейные непрерывные функционалы, т. е. операции сложения и умножения на число не выводят за пределы множества непрерывных функций. Понятие сходимости в множестве обобщённых функций определим следующим образом.
- линейные непрерывные функционалы, т. е. операции сложения и умножения на число не выводят за пределы множества непрерывных функций. Понятие сходимости в множестве обобщённых функций определим следующим образом.
Определение: Будем говорить, последовательность ![]() обобщённых функций сходится к обобщённой функции
обобщённых функций сходится к обобщённой функции ![]() , если
, если ![]() числовая последовательность
числовая последовательность ![]() при
при ![]() .
.
Линейное пространство обобщённых функций с введённой в нём сходимостью обозначается ![]() называется Пространством обобщённых функций. Введённое понятие сходимости называется «слабой сходимостью». Говорят также, что последовательность функционалов
называется Пространством обобщённых функций. Введённое понятие сходимости называется «слабой сходимостью». Говорят также, что последовательность функционалов ![]() слабо сходится к функционалу
слабо сходится к функционалу ![]() .
.
| < Предыдущая | Следующая > |
|---|