7.7. Регулярные и сингулярные обобщённые функции
Пусть функция ![]() локально интегрируемая функция.
локально интегрируемая функция.
Примеры: ![]() – локально интегрируемые, хотя и не интегрируемые на
– локально интегрируемые, хотя и не интегрируемые на ![]() . Каждой локально интегрируемой функции
. Каждой локально интегрируемой функции ![]() соответствует обобщённая функция (т. е. функционал)
соответствует обобщённая функция (т. е. функционал) ![]() , определённый равенством:
, определённый равенством: ![]() . Такие обобщённые функции называются Регулярными.
. Такие обобщённые функции называются Регулярными.
Примеры: ![]() – Функция Хевисайда.
– Функция Хевисайда.
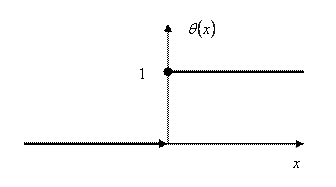
Функция ![]() порождает регулярную обобщённую функцию
порождает регулярную обобщённую функцию ![]() :
:  .Обобщённые функции, не являющиеся регулярными, называются Сингулярными.
.Обобщённые функции, не являющиеся регулярными, называются Сингулярными.
Пример: ![]() -функция. Она определяется в соответствие с равенством (4) из начала лекции:
-функция. Она определяется в соответствие с равенством (4) из начала лекции: ![]() . Докажем, что
. Докажем, что ![]() -функция является сингулярной обобщённой функцией. Допустим противное, тогда существует локально интегрируемая функция
-функция является сингулярной обобщённой функцией. Допустим противное, тогда существует локально интегрируемая функция ![]() такая, что:
такая, что: ![]() . Возьмём в качестве
. Возьмём в качестве![]() «шапочку»
«шапочку»  . Очевидно, что
. Очевидно, что ![]() По нашему предположению:
По нашему предположению:
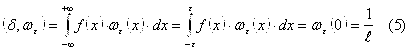
С другой стороны, т. к. ![]() локально интегрируема, то она ограничено на любом отрезке, и, следовательно,
локально интегрируема, то она ограничено на любом отрезке, и, следовательно,  при
при ![]() , что противоречит (5). Итак,
, что противоречит (5). Итак, ![]() -функция является сингулярной обобщённой функцией. Покажем, что
-функция является сингулярной обобщённой функцией. Покажем, что ![]() -функцию сингулярную обобщённую функцию можно представить как предел в
-функцию сингулярную обобщённую функцию можно представить как предел в ![]() регулярных обобщённых функций. Введём функционал
регулярных обобщённых функций. Введём функционал ![]() , где
, где ![]() - «шапочка»,
- «шапочка», ![]() - такое число, что
- такое число, что 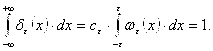 Т. к.
Т. к.  , то
, то ![]() . Поэтому
. Поэтому  . Регулярную обобщённую функцию, соответствующую
. Регулярную обобщённую функцию, соответствующую ![]() , обозначим
, обозначим ![]() . Докажем теперь, что
. Докажем теперь, что ![]()
![]() -функции при
-функции при ![]() в смысле сходимости в
в смысле сходимости в ![]() . Для этого нужно доказать, что
. Для этого нужно доказать, что ![]() такие, что
такие, что ![]() при
при ![]() Т. к.
Т. к. ![]() непрерывная функция, то
непрерывная функция, то ![]() такое, что
такое, что ![]() при
при ![]() Следовательно, при
Следовательно, при ![]() имеем:
имеем: 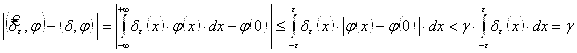 . Это означает, что
. Это означает, что![]() при
при ![]() , т. е.
, т. е. ![]() -функции при
-функции при ![]() в
в ![]() . Обратим внимание на поточечный предел:
. Обратим внимание на поточечный предел: ![]() – это не есть классическая функция.
– это не есть классическая функция. ![]() -функцию можно представить как предел многих других последовательностей регулярных обобщённых функций. Пусть
-функцию можно представить как предел многих других последовательностей регулярных обобщённых функций. Пусть  (ядро Дирихле порядка
(ядро Дирихле порядка ![]() ) и пусть
) и пусть ![]() . Так же, как и при доказательстве теоремы о поточечной сходимости тригонометрического ряда Фурье, нетрудно доказать, что
. Так же, как и при доказательстве теоремы о поточечной сходимости тригонометрического ряда Фурье, нетрудно доказать, что ![]()
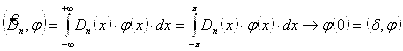 при
при ![]() . В самом деле, т. к.
. В самом деле, т. к. ![]() , то
, то  при
при ![]() . Это означает, что
. Это означает, что ![]() при
при ![]() в
в![]() Оказывается, что любую сингулярную обобщённую функцию можно представить как предел последовательности регулярных обобщённых функций иначе говоря пространство обобщённых функций является пополнением пространства классических локально интегрируемых функций, т. е. получается путём добавления к пространству классических локально интегрируемых функций всех предельных элементов в смысле слабой сходимости.
Оказывается, что любую сингулярную обобщённую функцию можно представить как предел последовательности регулярных обобщённых функций иначе говоря пространство обобщённых функций является пополнением пространства классических локально интегрируемых функций, т. е. получается путём добавления к пространству классических локально интегрируемых функций всех предельных элементов в смысле слабой сходимости.
(Аналогия: Множество всех вещественных чисел получается из множества рациональных чисел путём добавления всех пределов последовательностей рациональных чисел. Любое иррациональное число можно получить как предел последовательности рациональных чисел, поэтому все иррациональные числа окажутся добавленными по множеству рациональных чисел, т. е. множество всех вещественных чисел есть пополненные множества рациональных чисел.)
| < Предыдущая |
|---|