7.5. Преобразование Фурье

Интеграл Фурье: . Запишем интеграл Фурье в комплексной форме. Рассмотрим функцию . Эта функция является чётной функцией параметра 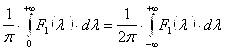, таким образом:

аналогично: – нечётная функция . Итак получаем:

Соотношение (3) называется комплексной формой интеграла Фурье. Перепишем формулу (3) в виде: 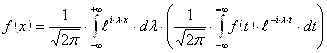и введём следующее обозначение: . Тогда соотношение (3) примет вид: . Функцию называют образом Фурье, – оригиналом Фурье, переход – обратным преобразованием Фурье, а переход – прямым преобразованием Фурье.

< Предыдущая		Следующая >