7.4. Интеграл Фурье

В том случае, когда функция является не периодической, для её представления используется интеграл Фурье. Рассмотрим ряд Фурье функции на сегменте :

где

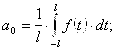
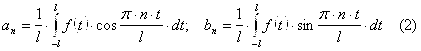
В физике выражение вида и называются гармониками, а само разложение функции (1) называется разложением функции по гармоникам. Введём, далее, выражение: – разность двух соседних частот. Нужно отметить, что при разность . От дискретного спектра разложения по частотам мы переходим к непрерывному спектру разложения по частотам.

Приближённый подход: Подставим выражения для интеграла Фурье (2) в формулу (1) и получим выражение для интеграла Фурье: 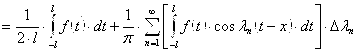. Перейдём к пределу при , при этом будем считать функцию абсолютно интегрируемой, т. е. – сходится, тогда: – интеграл Фурье.

Рассмотрим теперь строгий подход.

Теорема: Если функция :

1. Определена на всей числовой прямой ;

2. Кусочно-гладкая на всей числовой прямой ;

3. Абсолютно интегрируема на всей числовой прямой , то для любого справедливо равенство: .

Док-во: Согласно определению несобственного интеграла перепишем интеграл в левой части: . Нам нужно доказать, что . Внутренний интеграл представляет собой несобственный интеграл, зависящий от параметра и сходящийся равномерно по параметру при . Это справедливо в силу мажорантного признака Вейерштрасса: . Поэтому можно изменить в интеграле порядок интегрирования по и : . Это даёт, что . Воспользуемся изменённым соотношением (а именно разрывным множителем Дирихле): 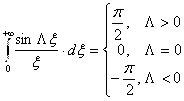. При имеем: . Вычитая это равенство из равенства , получим: . Зададим и возьмём достаточно большим так, чтобы выполнялось неравенство: . Такая оценка возможно, т. к. интеграл является сходящимся. По Лемме 2: для любого фиксированного A: при существует : при . Наконец: – сходится существует такое : при . Следовательно, при при , т. к. при , аналогично при , ч. т.д.

< Предыдущая		Следующая >