7.3. Замкнутые и полные ортонормированные системы

Ключевым моментом для построения рядов Фурье является корректность выбора ортонормированной системы .

Определение: Ортонормированная система в бесконечномерном евклидовом пространстве называется замкнутой, если любой элемент этого пространства можно приблизить с произвольной точностью по норме данного пространства с помощью конечной линейной комбинации элементов : и .

Теорема 2: (Необходимое и достаточное условие замкнутости ортонормированной системы). Для того чтобы ортонормированная система была замкнута, необходимо и достаточно, чтобы для любого элемента :

Где . (Равенство (1) называется Равенством Парсеваля).

Док-во:

1. (Необходимость) Воспользуемся Тождеством Бесселя. Если система – замкнутая, то такое, что левая часть тождества будет меньше чем при .

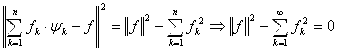2. (Достаточность) Если справедливо Равенство Парсеваля, то такое, что правая часть тождества будет меньше, чем , следовательно, и левая часть тождества будет меньше чем . А последнее означает, что система будет замкнутой, ч. т.д.

< Предыдущая		Следующая >