7.2. Понятие общего ряда Фурье

Тригонометрический ряд Фурье является частичным случаем общего ряда Фурье. Понятие общего ряда Фурье связано с разложением бесконечномерного евклидова пространства по ортонормированной системе. Будем рассматривать бесконечномерное евклидово пространство, т. е. линейное пространство, в котором имеется в том числе и бесконечно большое число независимых элементов , с точки зрения функций тригонометрической системы.

Пример: Рассмотрим пространство кусочно-непрерывных на сегменте функций (Обозначение: , ). Будем предполагать, что в точке разрыва . Введём в пространстве скалярное произведение (свёртку) двух функций: . СкалярноеПроизведение удовлетворяет следующему свойству: (данное неравенство называется Неравенством Коши-Буняковского).

Определение: Линейное пространство называется нормированным, если каждому элементу поставлено в соответствие неотрицательное вещественное число – норма элемента . Причём норма удовлетворяет следующим условиям:

1. , если ; , если ;

2. , для любого ;

3. .

Примечание: Отметим, что в любом нормированном пространстве можно ввести метрику – расстояние между двумя элементами, в данном случае . Во всяком евклидовом пространстве можно ввести норму из скалярного произведения: .

Определение: Последовательность элементов евклидова пространства называется ортонормированным, если её элементы являются попарно ортогональны, а норма каждого элемента равна единице.

Определение: Рядом Фурье элемента F по ортонормированной системе называется ряд , где . называется коэффициентом Фурье элемента F.

Если евклидово пространство имеет конечную размерность равную , то система , состоящая из ортогональных элементов, норма каждого из которых равна единице, образует ортонормированный базис и любой элемент F такого пространства можно разложить по этому базису: . Указанное разложение также представляет собой пример общего ряда Фурье, но только этот ряд содержит конечное число слагаемых. В случае бесконечной размерности евклидова пространства встаёт вопрос о сходимости ряда Фурье, рассматривается сходимость к элементу пространства F по метрике данного пространства. Рассмотрим сумму . Назовём её N-ой частичной суммой ряда Фурье. Наряду с будем рассматривать линейные комбинации элементов ортонормированной системы .

Теорема 1: При фиксированном Из всех сумм вида наименьшее отклонение элемента по норме данного евклидова пространства имеет N-ая частичная сумма (частичная сумма ряда Фурье). Или частичная сумма выражает свойство «экстремальности» ряда Фурье (минимизация погрешности приближения данного элемента F).

Док-во: Рассмотрим , получаем:

(прибавим и вычтем )

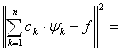
. Таким образом наименьшее отклонение от элемента по норме данного пространства даёт наименьшее отклонение, ч. т.д.

Утверждения:

1. Для любого элемента , для любой ортонормированной системы и для любого выполняется равенство: (данное равенство называется Тождеством Бесселя).

2. Для любого элемента , для любой ортонормированной системы справедливо равенство: .

< Предыдущая		Следующая >