4. Несобственные интегралы. Несобственные интегралы I рода

Пусть функция определена на полупрямой . Будем полагать, что 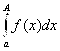Указанный интеграл зависит от A, то есть является функцией аргумента А.

Рассмотрим .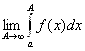

Этот предел может существовать, а может и не существовать. Но независимо от этого будем обозначать его, 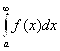и называть его несобственным интегралом первого рода.

В том случае, если предел существует, несобственный интеграл первого рода называется сходящимся, если предел не существует – расходящимся.

Пример 1:

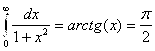
Пример 2:

не существует, исходный интеграл – расходящийся.

Пример 3:

Т. е. интеграл является сходящимся при и расходящимся при .

Не всегда удается вычислить соответствующий определенный интеграл в элементарных функциях, поэтому исследовать несобственный интеграл на сходимость напрямую не всегда удается. В связи с этим, пример:

Пример 4:

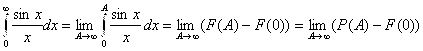, где – первообразная.

< Предыдущая		Следующая >