4.1. Признаки сходимости несобственных интегралов I рода
Теорема 1 (Критерий Коши сходимости несобственных интегралов первого рода): Для того чтобы несобственный интеграл 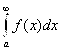 сходился необходимо и достаточно, чтобы
сходился необходимо и достаточно, чтобы ![]() выполняется неравенство
выполняется неравенство 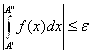
Док-во: Обозначим функцией ![]() Интеграл
Интеграл 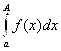 то есть
то есть 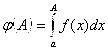 .
.
По определению сходимость несобственного интеграла 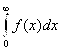 означает существование
означает существование ![]() .
.
В свою очередь, для того чтобы существовал этот предел необходимо и достаточно, чтобы ![]() выполняется следующее неравенство
выполняется следующее неравенство
![]() , но
, но 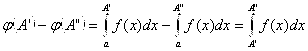 , таким образом, получаем, что
, таким образом, получаем, что ![]() выполняется
выполняется , ч. т.д.
, ч. т.д.
Вернемся к примеру 4. Рассмотрим следующий интеграл

Зададим ![]() и выберем
и выберем ![]() , по критерию Коши исходный несобственный интеграл первого рода
, по критерию Коши исходный несобственный интеграл первого рода 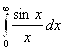 сходится.
сходится.
Теорема 2: (признак сравнения) Пусть ![]() при
при ![]() И функции
И функции ![]() и
и ![]() интегрируемые функции на любом сегменте
интегрируемые функции на любом сегменте ![]() , тогда из сходимости интеграла
, тогда из сходимости интеграла
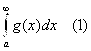
Следует сходимость интеграла
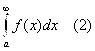
А из расходимости (2) следует расходимость интеграла (1).
Док-во: ![]() введём две функции
введём две функции
 и
и 
Эти функции подчиняются такому соотношению

Из последней записи следует, что если интеграл (1) сходится, то функция ![]() – ограниченная, поэтому функция
– ограниченная, поэтому функция ![]() также будет ограниченной и, следовательно, интеграл (2) сходится. Если же интеграл (1) расходится, то функция
также будет ограниченной и, следовательно, интеграл (2) сходится. Если же интеграл (1) расходится, то функция ![]() неограниченна, поэтому функция
неограниченна, поэтому функция ![]() также неограниченна и значит интеграл (1) является расходящимся, ч. т.д.
также неограниченна и значит интеграл (1) является расходящимся, ч. т.д.
Следствия:
1) ![]() при
при ![]() , то
, то 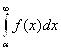 сходится при
сходится при ![]() , если
, если ![]() то
то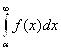 расходится при
расходится при ![]() .
.
2) ![]() и
и ![]() при
при ![]()
![]()
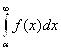 и
и 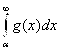 то интегралы сходятся и расходятся при этом одновременно.
то интегралы сходятся и расходятся при этом одновременно.
Пример: 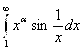 ; 0
; 0![]() при
при ![]() Получаем:
Получаем: ![]() рассмотрим
рассмотрим
Следующий предел: 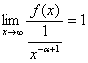 так как
так как ![]() исходный интеграл сходится и расходится одновременно с интегралом:
исходный интеграл сходится и расходится одновременно с интегралом: 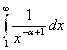 .
.
Сходится при ![]() , расходится при
, расходится при ![]() .
.
| < Предыдущая | Следующая > |
|---|