3.7. Сходимость в среднем
Рассмотрим координатное пространство EM и рассмотрим две точки из этого пространства ![]() и рассмотрим
и рассмотрим ![]() .
.
Определение: Если на некотором множестве задана функция расстояния![]() , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) ![]() , причем
, причем ![]() Если
Если ![]() ;
;
2) ![]()
3) ![]()
То говорят, что на данном множестве введена метрика, а само множество называется метрическим пространством.
Для последовательности точек в координатном пространстве {MN}![]() M, при
M, при ![]()
![]() означает, что расстояние между любой точкой последовательности
означает, что расстояние между любой точкой последовательности ![]() В этом случае говорят, что имеется сходимость в метрике этого пространства. Природа элементов метрического пространства может быть весьма разнообразна (например, функции). Введем метрику на множестве функций в метрическом пространстве.
В этом случае говорят, что имеется сходимость в метрике этого пространства. Природа элементов метрического пространства может быть весьма разнообразна (например, функции). Введем метрику на множестве функций в метрическом пространстве.
Пример 1: Рассмотрим множество всевозможных ограниченных функций на сегменте ![]() . Введем метрику следующим образом:
. Введем метрику следующим образом: ![]() . Можно проверить, что функция
. Можно проверить, что функция ![]() удовлетворяет трем вышеперечисленным условиям. Сходимость
удовлетворяет трем вышеперечисленным условиям. Сходимость ![]() при
при ![]() в метрике данного пространства означает, что
в метрике данного пространства означает, что ![]() при
при ![]() (равномерная сходимость), то есть сходимость в метрике рассматриваемого пространства соответствует ранее введенному понятию равномерной сходимости.
(равномерная сходимость), то есть сходимость в метрике рассматриваемого пространства соответствует ранее введенному понятию равномерной сходимости.
Пример 2: Рассмотрим множество кусочно-непрерывных функций на сегменте ![]() , удовлетворяющих в точках разрыва следующему условию:
, удовлетворяющих в точках разрыва следующему условию: ![]() .
.
Для данного множества функций введем:  .
.
Можно проверить, что введенная таким образом функция ![]() Удовлетворяет трем условиям функции расстояния. А введенное условие точки разрыва позволяет избежать ситуации
Удовлетворяет трем условиям функции расстояния. А введенное условие точки разрыва позволяет избежать ситуации![]() при
при ![]() . Сходимость
. Сходимость ![]() к
к ![]() означает, что
означает, что 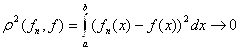 при
при ![]() . Такая сходимость называется сходимостью в среднем. Введенное ограничение на значение функции в точках разрыва гарантирует, что предельная функция
. Такая сходимость называется сходимостью в среднем. Введенное ограничение на значение функции в точках разрыва гарантирует, что предельная функция ![]() при сходимости в среднем будет определяться единственным образом.
при сходимости в среднем будет определяться единственным образом.
Определение: Пусть функции ![]() и
и ![]() интегрируемы на сегменте
интегрируемы на сегменте ![]() , говорят, что функциональная последовательность
, говорят, что функциональная последовательность ![]() сходится в среднем к функции
сходится в среднем к функции ![]() на сегменте
на сегменте ![]() , если
, если 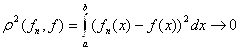 при
при ![]() .
.
Теорема 7: Пусть функции ![]() и
и ![]() интегрируемы на сегменте
интегрируемы на сегменте ![]() , если функциональная последовательность
, если функциональная последовательность ![]() на сегменте
на сегменте ![]() , то
, то ![]() в среднем не сегменте
в среднем не сегменте ![]() .
.
Док-во: Зададим некоторое достаточно малое значение ![]() , так как
, так как ![]() на
на ![]() , то
, то ![]() такое, что
такое, что![]() ,
, ![]() справедливо неравенство
справедливо неравенство ![]() .
.
Поэтому ![]() :
: 
![]()
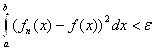 .
.
Это означает, что ![]() При
При ![]() , то есть мы имеем сходимость в указанной метрике или последовательность
, то есть мы имеем сходимость в указанной метрике или последовательность ![]() в среднем, ч. т.д.
в среднем, ч. т.д.
Замечание: Обратное утверждение не верно, более того из сходимости в среднем, не следует обычная (поточечная) сходимость.
Пример 3: ![]() на
на ![]() , функции
, функции
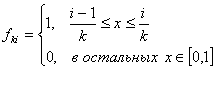
![]()
Надо доказать, что ![]() в среднем на
в среднем на ![]() .
.
 При
При ![]() .
.
Поэтому функциональная последовательность ![]() сходится к функции
сходится к функции ![]() в среднем на сегменте
в среднем на сегменте ![]() . Но заметим, что ни в одной точке на
. Но заметим, что ни в одной точке на ![]() функциональная последовательность
функциональная последовательность ![]() не является сходящейся, так как
не является сходящейся, так как ![]() . Таким образом функциональная последовательность
. Таким образом функциональная последовательность ![]() будет состоять из бесконечного числа нулей и бесконечного числа единиц, то есть не будет сходиться. Из поточечной сходимости функциональной последовательности
будет состоять из бесконечного числа нулей и бесконечного числа единиц, то есть не будет сходиться. Из поточечной сходимости функциональной последовательности ![]() на
на ![]() не следует сходимость в среднем.
не следует сходимость в среднем.
Пример 4:
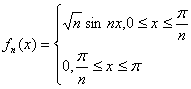
![]() при
при ![]() , то есть на сегменте
, то есть на сегменте ![]() имеет место поточечная сходимость. Но при этом
имеет место поточечная сходимость. Но при этом
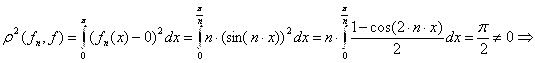
Сходимости в среднем не имеет место быть.
Определение: Говорят, что функциональный ряд ![]() сходится в среднем и
сходится в среднем и ![]() на сегменте
на сегменте ![]() , если последовательность его частичных сумм
, если последовательность его частичных сумм ![]() Сходится в среднем к
Сходится в среднем к ![]() на
на ![]() , то есть
, то есть
 при
при ![]()
Сходимость в среднем представляет собой более слабое условие, чем равномерная сходимость, но, наряду с этим, является достаточным условием перехода к пределу под знаком интеграла, а сходимость в среднем для функциональных рядов является достаточным условием почленного интегрирования функционального ряда.
Теорема 8: Пусть функции ![]() и
и ![]() интегрируемы на
интегрируемы на ![]() . Пусть функциональная последовательность
. Пусть функциональная последовательность ![]() сходится в среднем к
сходится в среднем к ![]() на
на ![]() , тогда
, тогда ![]()

Причем для любого фиксированного ![]() верно
верно  на
на ![]() .
.
Доказательство:
По условию теоремы 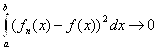 при
при ![]()
Следовательно,  на
на ![]() .
.

Рассмотрим интеграл 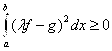
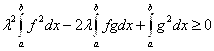
Воспользуемся неравенством Коши-Буняковского
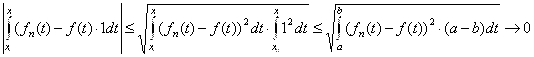 при
при ![]()
Зададим![]() , тогда
, тогда ![]() правая часть полученного неравенства будет меньше чем
правая часть полученного неравенства будет меньше чем![]() . Тем самым
. Тем самым ![]() из сегмента
из сегмента ![]() .
.
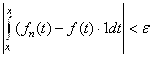
![]()
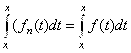 , ч. т.д.
, ч. т.д.
Теорема 8’: Если функциональный ряд сходится в среднем на сегменте ![]() к функции
к функции ![]() и если все функции
и если все функции ![]() И
И ![]() интегрируемы на сегменте
интегрируемы на сегменте ![]() , то
, то ![]()

То есть функциональный ряд можно интегрировать почленно, причем
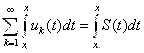 на
на ![]() .
.
В доказательстве Теоремы 6’ условие 3 заменяется на условие, что ряд ![]()
Сходится в среднем на сегменте ![]() к некоторой непрерывной функции
к некоторой непрерывной функции ![]() .
.
Теорема Арцела
Определение: Функциональная последовательность ![]() Называется равномерно ограниченной на множестве Х, если
Называется равномерно ограниченной на множестве Х, если ![]()
Определение: Функциональная последовательность {fn(x)}называется равномерно непрерывной на Х, если ![]()
Теорема (теорема Арцела): Если функциональная последовательность равномерно ограничена и
Равномерно непрерывна на сегменте ![]() , то из нее можно выделить подпоследовательность, равномерно сходящуюся на сегменте
, то из нее можно выделить подпоследовательность, равномерно сходящуюся на сегменте ![]() .
.
| < Предыдущая | Следующая > |
|---|