3.6. Переход к пределу под знаком производной и почленное дифференцирование ряда

Пусть на множестве Х. Пусть функции и дифференцируемы на сегменте . Поставим вопрос: сходится ли последовательности и .

Теорема 6: Пусть

Функции имеют непрерывные производные на сегменте .

на сегменте . на .

Тогда:

Функция дифференцируема на сегменте . , т. е. .

Док-во: Т. к. На , то по Теореме 4 функция является непрерывной на сегменте , по Теореме 3:

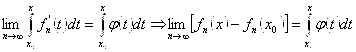
Таким образом, получаем, что функция является дифференцируемой функцией: , ч. т.д.

Теорема 6’: Пусть:

Все функции имеют непрерывные производные на сегменте . сходится к на сегменте . сходится равномерно к на сегменте .

Тогда функция – дифференцируемая функция на сегменте , причем , или

.

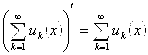Док-во: Доказательство теоремы сводится к доказательству Теоремы 6.

< Предыдущая		Следующая >