3.5. Переход к пределу под знаком интеграла и почленное интегрирование ряда

Пусть на множестве Х. Пусть точки X и – две произвольные точки из множества Х. Рассмотрим два интеграла:

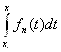и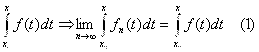

Иными словами верно ли равенство

Пример: при на .

.

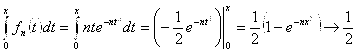Аналогичный вопрос ставится и для сходящегося числового ряда. Если последнее равенство верно, то говорят, что ряд можно интегрировать почленно от X до . Корректный переход к пределу под знаком интеграла возможен в том случае, если имеется равномерная сходимость соответствующей последовательности или ряда.

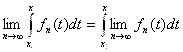Теорема 5: Пусть функция – непрерывны на сегменте . Пусть равномерно сходится к на сегменте . Тогда для любых X, , причем на , для любого .

Док-во: По определению равномерной сходимости нам надо доказать, что

.

Зададим , т. к. равномерно сходится к на , то и

. Оценим разность интегралов . Отметим, что функция – Непрерывная функция на сегменте . Тогда и

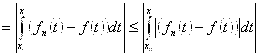, перепишем в следующем виде:

. Последнее означает, что 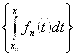равномерно сходится к, ч. т.д.

Теорема 5’: Если все функции непрерывны на сегменте и , то

.Т. е. при указанных условиях функциональный ряд надо интегрировать почленно.

< Предыдущая		Следующая >