4.5. Несобственные кратные интегралы
Несобственный интеграл возникает на неограниченной области, либо ограниченной области, но имеющей особые точки. Пусть G – ограниченная квадрируемая область на плоскости ![]() , и пусть в области G (за исключением, быть может, некоторой точки
, и пусть в области G (за исключением, быть может, некоторой точки![]() ) определена функция
) определена функция ![]() , не ограниченная в окрестности точки
, не ограниченная в окрестности точки ![]() . Заключим точку
. Заключим точку![]() В произвольную квадрируемую область
В произвольную квадрируемую область![]() , где
, где ![]() – диаметр области
– диаметр области ![]() . Пусть функция
. Пусть функция ![]() интегрируема в области
интегрируема в области ![]() . Рассмотрим предел на области
. Рассмотрим предел на области ![]() .
.
![]() .
.
Этот предел называется несобственным интегралом от функции ![]() по области G (несобственный двойной интеграл). Для кратных несобственных интегралов, как правило, не вводят понятия интегралов первого и второго рода. Если указанный предел существует и не зависит от способа стягивания области
по области G (несобственный двойной интеграл). Для кратных несобственных интегралов, как правило, не вводят понятия интегралов первого и второго рода. Если указанный предел существует и не зависит от способа стягивания области ![]() точке
точке![]() , то говорят, что несобственный интеграл сходится, а в противном случае – расходится. В ряде задач математической физики важную роль играет случай, когда
, то говорят, что несобственный интеграл сходится, а в противном случае – расходится. В ряде задач математической физики важную роль играет случай, когда![]() – круг с радиусом
– круг с радиусом ![]() И центром в точке
И центром в точке![]() . Если существует
. Если существует
![]() , где
, где ![]() – круг с радиусом
– круг с радиусом ![]() И центром в точке
И центром в точке![]() , то этот предел называется главным значением несобственного интеграла по области G от функции
, то этот предел называется главным значением несобственного интеграла по области G от функции ![]() и обозначается
и обозначается
V.P. ![]()
Пусть функция ![]() определена в неограниченной области G и пусть последовательность
определена в неограниченной области G и пусть последовательность ![]() ограниченных квадрируемых областей монотонно «исчерпывает» область G, то есть любая область
ограниченных квадрируемых областей монотонно «исчерпывает» область G, то есть любая область![]() и
и ![]()
Пусть функция ![]() интегрируема в любой ограниченной области вида
интегрируема в любой ограниченной области вида ![]() . Рассмотрим числовую последовательность
. Рассмотрим числовую последовательность ![]() , построенную следующим образом
, построенную следующим образом ![]() . Если
. Если ![]()
![]() и не зависит от выбора последовательности областей
и не зависит от выбора последовательности областей ![]() ,то говорят, что несобственный интеграл
,то говорят, что несобственный интеграл ![]() сходится, а в противном случае – расходится.
сходится, а в противном случае – расходится.
Замечание: Кратные несобственные интегралы обладают следующим удивительным свойством, а именно: для несобственных интегралов понятия сходимости и абсолютной сходимости являются эквивалентными.
Отмеченное свойство обусловлено произвольностью стягивания ![]() К точке
К точке![]() , или соответственно, произвольностью выбора последовательности
, или соответственно, произвольностью выбора последовательности ![]()
Пример 1: ![]() . Точка
. Точка![]() Является внутренней точкой области G, а точка М – произвольная точка области G, то есть точка является особой точкой. Выберем какую-либо окрестность
Является внутренней точкой области G, а точка М – произвольная точка области G, то есть точка является особой точкой. Выберем какую-либо окрестность![]() точки
точки ![]() .Обозначим эту окрестность
.Обозначим эту окрестность![]() . В области
. В области ![]() функция
функция ![]() Ограничена
Ограничена ![]() , поэтому интеграл
, поэтому интеграл ![]() . Выберем область
. Выберем область ![]() (произвольная),
(произвольная), ![]() – ее диаметр. Поэтому
– ее диаметр. Поэтому ![]() В области
В области ![]() Является положительной. Оказывается, если
Является положительной. Оказывается, если ![]() , то для сходимости несобственного интеграла по области G
, то для сходимости несобственного интеграла по области G ![]() необходимо и достаточно, чтобы
необходимо и достаточно, чтобы ![]() существовал. Воспользуемся этим и выберем в качестве
существовал. Воспользуемся этим и выберем в качестве![]() Круг радиуса
Круг радиуса ![]() С центром в точке
С центром в точке![]() . Для вычисления
. Для вычисления ![]() Перейдем к полярной системе координат с центром в точке
Перейдем к полярной системе координат с центром в точке ![]() .
.
Тогда получаем 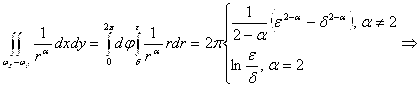
![]()
не существует при ![]() , при
, при ![]() – существует.
– существует.
Пример 3: ![]() ;
;![]() .
.
Перейдем к полярным координатам и тогда получим
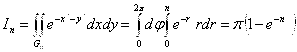 .
.
Используем для вычисления интеграл Пуассона. В качестве областей ![]() Будем выбирать квадраты
Будем выбирать квадраты
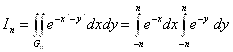 ;
;![]()
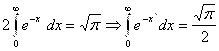 .
.
| < Предыдущая | Следующая > |
|---|