4.4. Главное значение несобственного интеграла

Пример:

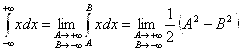
Полученный предел очевидно не существует. Пусть, тогда указанный интеграл:

Пусть определена на И пусть функция интегрируема на любом сегменте.

Определение: Если существует предел , то он называется главным значением несобственного интеграла в смысле Коши и обозначается следующим образом:

(V.P. = Vabeur principal).

В этом случае говорят, что функция интегрируема на прямой . Очевидно, что если несобственный интеграл сходится, то его значение совпадает с его собственным значением. Но может так быть, что несобственный интеграл расходится, но при этом имеет конечное главное значение.

Рассмотрим несобственный интеграл второго рода 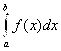, где C – внутренняя особая точка интервала .

Определение: Если существует предел «конструкции» следующего вида: ,

То он называется главным значением несобственного интеграла второго рода 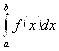И обозначается V.P. .

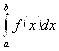Отметим, что исходный несобственный интеграл может быть расходящимся, то есть может не существовать предел .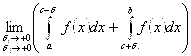

Пример:

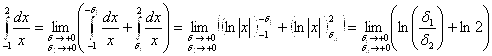не существует.

Вычислим интеграл в смысле главного значения:

V.P. .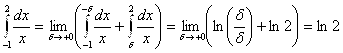

< Предыдущая		Следующая >