4.6. Собственные интегралы, зависящие от параметра
1. ![]() .
.
2. ![]() ;
; ![]() .
.
3. A, B – множители;![]() .
.
4. A, B – множители; F: ![]() ; f – отображение
; f – отображение ![]() .
.
5.![]() – плотное в себе множество
– плотное в себе множество ![]() и
и ![]() [окрестность точки]
[окрестность точки] ![]() .
.
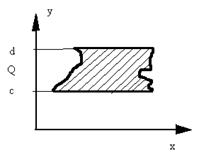 Пусть имеется множество Q в N-мерном пространстве
Пусть имеется множество Q в N-мерном пространстве ![]() и в нем заданы функции
и в нем заданы функции ![]() ,
, ![]() , причем
, причем ![]() и
и ![]() такие, что
такие, что ![]() . Пусть в
. Пусть в ![]() :
: ![]() .Рассмотрим случай когда
.Рассмотрим случай когда ![]() ,
, ![]() – следовательно,
– следовательно, ![]() : F:
: F:![]() интеграл по X на
интеграл по X на ![]()
![]()
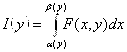 .
.
И этот интеграл называется собственным интегралом, зависящим от параметра.
Теорема 1 (Теорема о непрерывности): Пусть Q – параллелепипед в N-мерном пространстве: ![]() .
.
Вместо параллелепипеда может быть замкнутое, ограниченное, плотное в себе множество  при
при ![]() .
.
Теорема 1.1:
Пусть ![]() непрерывна в области определения. Тогда
непрерывна в области определения. Тогда ![]() непрерывна в своей области определения
непрерывна в своей области определения ![]() .
.
Док-во: ![]()
![]()
![]() ;
;![]() при
при ![]()
![]()
![]() Где
Где ![]() Фиксируем
Фиксируем ![]() , тогда по первой теореме Вейерштрасса можно указать такое число
, тогда по первой теореме Вейерштрасса можно указать такое число ![]() , что
, что ![]() При
При ![]() по теореме Кантора функция F равномерно непрерывна на сегменте
по теореме Кантора функция F равномерно непрерывна на сегменте ![]() , можно указать такое
, можно указать такое ![]() , что выполняется:
, что выполняется:
![]() при
при ![]() .Фиксируем
.Фиксируем ![]() ,
, ![]() ,
, 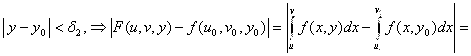
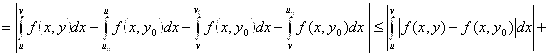
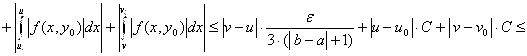
![]()
![]() , ч. т.д.
, ч. т.д.
Уточним Теорему 1.1: Пусть ![]() при
при ![]() и соответственно
и соответственно 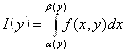 .
.
Теорема 1.2: Пусть функция ![]() непрерывна на прямоугольнике
непрерывна на прямоугольнике ![]() . Обозначим:
. Обозначим:
 ;
; 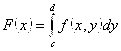 .
.
Тогда:
1. Функция ![]() непрерывна на сегменте
непрерывна на сегменте ![]()
![]() .
.
2. Функция ![]() .
.
3.  , тогда
, тогда 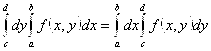 .
.
Док-во: По Теореме 1.2: ![]() ,
, ![]() ;
; 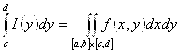
 , ч. т.д.
, ч. т.д.
Теорема 1.4:
Пусть функция F непрерывна в области определения ![]() , пусть также существует производная
, пусть также существует производная ![]() и
и ![]() непрерывна также на
непрерывна также на ![]() .
.
Тогда:
1. ![]() , где
, где ![]() – множество непрерывных функций, имеющих непрерывные первые производные.
– множество непрерывных функций, имеющих непрерывные первые производные.
2. ![]()
![]()
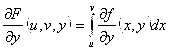 .
.
Док-во:  ;
; 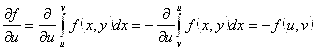
![]()
![]() И
И![]() непрерывные (т. к.
непрерывные (т. к. ![]() – непрерывная функция). Введем следующую вспомогательную функцию, которую назовем «формальной» производной:
– непрерывная функция). Введем следующую вспомогательную функцию, которую назовем «формальной» производной:
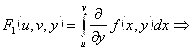
 фиксируем
фиксируем ![]()
![]() получаем:
получаем: 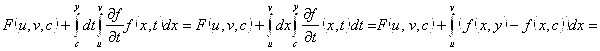
![]()
![]()
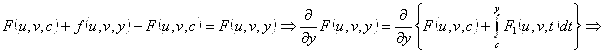
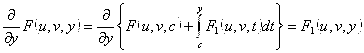 , ч. т.д.
, ч. т.д.
Теорема 1.5: Пусть F, ![]() Дифференцируемы на
Дифференцируемы на ![]() .
.
Тогда:
1. I – дифференцируема на ![]() .
.![]() .
.
2. 
Док-во:![]() I – дифференцируема.
I – дифференцируема. ![]()
![]()
 , ч. т.д.
, ч. т.д.
| < Предыдущая | Следующая > |
|---|