16. Квадратурные формулы численного интегрирования

В прикладных исследованиях, когда возникает необходимость вычисления и первообразной не существует, приходиться интеграл считать численно. Наиболее широко на практике используются квадратурные формулы - приближенные равенства вида

(4.5.1)

Где - некоторые точки из отрезка - узлы квадратурной формулы (4.5.1), - числовые коэффициенты, называемые весами квадратурной формулы, - целое число. Сумма , которая принимается за приближенное значение интеграла, называется квадратурной суммой.

Величина 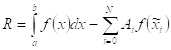называется погрешностью или остаточным членом квадратурной формулы. Выведем простейшие квадратурные формулы, исходя из геометрической интерпретации определенного интеграла:

Будем интерпретировать интеграл как площадь криволинейной трапеции, ограниченной графиком функции , осью абсцисс и прямыми Разобьем отрезок на элементарные отрезки точками Интеграл представится таким образом:

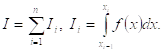(4.5.2)

Введем обозначения: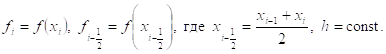

Формула центральных прямоугольников. Заменим приближенно площадь элементарной криволинейной трапеции площадью прямоугольника, основанием которого является отрезок , а высота равна значению . Тогда сразу получается элементарная квадратурная формула прямоугольников Суммируя по всему отрезку , получим

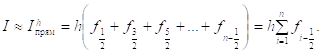(4.5.3)

Совершенно аналогично можно получить формулы и , которые называются квадратурными формулами левых и правых прямоугольников. Их точность , тогда как точность формулы (4.5.3) .

Формула трапеций. Соединив точки , получим формулу трапеций.

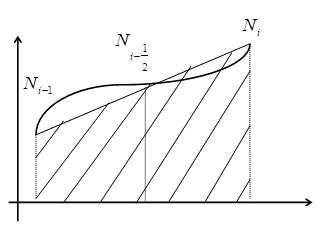
Заменим площадь элементарной криволинейной трапеции площадью построенной фигуры. Тогда , а итоговая формула примет вид

(4.5.4)

Формула парабол (Симпсона). Если площадь элементарной криволинейной трапеции заменить площадью фигуры, расположенной под параболой, проходящей через точки , то получим приближенное равенство - интерполяционный многочлен второй степени с узлами

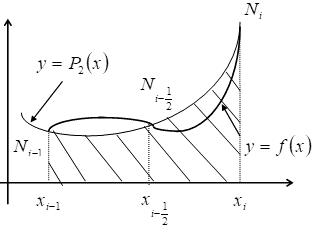
Для этих точек справедлива формула

Квадратурная формула парабол (Симпсона)

< Предыдущая		Следующая >