15. Формулы численного дифференцирования для второй производной
Наиболее простой и широко применяемой для приближенных вычислений второй производной является следующая формула
![]() (4.2.1)
(4.2.1)
Она выводится из формулы ![]() , в которой первые производные рассчитываются по формуле (4.2.1) по трем точкам
, в которой первые производные рассчитываются по формуле (4.2.1) по трем точкам ![]() . Формулу (4.2.1) часто называют второй разностной производной. Покажем, что она имеет второй порядок точности относительно
. Формулу (4.2.1) часто называют второй разностной производной. Покажем, что она имеет второй порядок точности относительно ![]() . Итак,
. Итак, ![]() причем
причем ![]() Тогда
Тогда

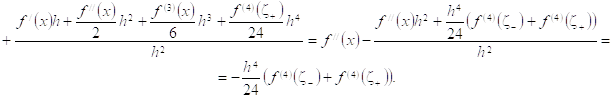 Следовательно,
Следовательно, ![]() (4.2.2)
(4.2.2)
Для получения ![]() можно использовать формулы любого порядка точности. Например, формула
можно использовать формулы любого порядка точности. Например, формула ![]() (4.2.3)
(4.2.3)
Имеет четвертый порядок точности относительно параметра ![]() , но требует наличия значений функции в пяти точках.
, но требует наличия значений функции в пяти точках.
| < Предыдущая | Следующая > |
|---|