11. Многочлены Чебышева и их свойства

Система функций , заданных на , называется ортогональной на , если

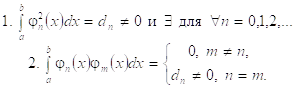(3.5.1)

Система функций , заданных на , называется ортогональной на с весом , если

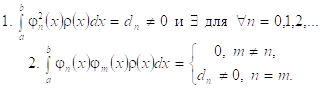(3.5.2)

Функция называется весовой функцией для системы . Если , то система функций называется ортонормированной.

В качестве примера системы функций, ортогональной с весом, приведем многочлены Чебышева, которые известны еще и тем, что являются полиномами, наименее уклоняющимися от нуля. Эти многочлены определяют разными способами. Например:

(3.5.3)

2. Являются решениями следующего дифференциального уравнения:

(3.5.4)

3. Определяются из формулы Родрига

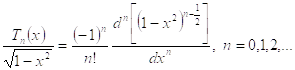(3.5.5)

4. Определяются рекуррентно:

(3.5.6)

Иногда в качестве полиномов Чебышева берут функции

. (3.5.7)

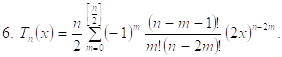(3.5.8)

Многочлены Чебышева обладают множеством замечательных свойств.

Теорема 3.4. Полиномы Чебышева образуют на отрезке ортогональную систему с весом

Теорема 3.5. При четном многочлен содержит только четные степени и является четной функцией, а при нечетном многочлен содержит только нечетные степени и является нечетной функцией.

Теорема 3.6. При старший коэффициент многочлена равен , то есть

Теорема 3.7. При многочлен имеет ровно действительных корней, расположенных на отрезке и вычисляемых по формуле

(3.5.10)

Теорема 3.8. При справедливо равенство . Если , то этот максимум достигается ровно в точках, которые находятся по формуле

(3.5.11)

При этом , то есть максимумы и минимумы многочлена Чебышева чередуются.

Теоремы 3.7 и 3.8 легко доказываются с помощью формулы (3.5.7).

Назовем величину уклонением многочлена от нуля. Тогда справедлива следующая, доказанная П. Л. Чебышевым в 1854 г. теорема.

Теорема 3.9. Среди всех многочленов фиксированной степени со старшим коэффициентом , равным единице, наименьшее уклонение от нуля, равное , имеет многочлен

< Предыдущая		Следующая >