09. Интерполяционный многочлен Ньютона

Пусть функция задана в точках таблично, то есть известны

			...
			...

Алгебраический многочлен -й степени

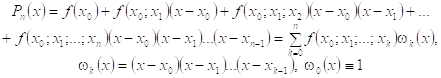(2.7.1)

Называется интерполяционным многочленом Ньютона с разделенными разностями. Очевидна аналогия формулы (2.7.1) с формулой Тейлора. Действительно, так как по теореме 2.7 то Формулы подраздела 2.4 о погрешности интерполяции в точке , не являющейся узловой, можно уточнить следующим образом: (2.7.2)

В практическом плане формула (2.7.1) обладает рядом преимуществ перед формулой Лагранжа. Если, например, по каким-либо причинам необходимо увеличить степень интерполяционного многочлена на единицу, добавив в таблицу еще один узел , то при использовании формулы Лагранжа это приведет не только к увеличению числа слагаемых, но и к необходимости вычислять каждое из них заново. В то же время для вычисления по формуле Ньютона (2.7.1) достаточно добавить к лишь очередное слагаемое, так как Если величина мала, а функция достаточно гладкая, то справедлива оценка: из которой, с учетом предыдущего равенства, следует, что Тогда величину

(2.7.3)

Можно использовать для практической оценки погрешности интерполяции.

< Предыдущая		Следующая >