08. Разделенные разности и их свойства

Пусть функция задана на таблице значений аргумента с произвольным шагом, причем точки таблицы занумерованы также в произвольном порядке.

Величины называются разделенными разностями первого порядка функции в узлах Аналогично определяются разделенные разности более высокого порядка: - Разделенная разность второго порядка в узлах Разделенной разностью -Го порядка называется число

(2.6.1)

Эти разности также можно записывать в виде треугольной таблицы:

Разделенные разности обладают рядом замечательных свойств, изложенных в следующих теоремах.

Теорема 2.5. Разделенная разность является симметричной функцией своих аргументов (то есть ее свойства не меняются при любой их перестановке).

Теорема 2.6. Разделенная разность -го порядка выражается через значения функции следующим образом

(2.6.2)

Легко заметить, что под знаком суммы стоят коэффициенты обобщенного многочлена , которые мы получали при выводе формулы Лагранжа (2.3.3). Теорема 2.6 доказывается методом математической индукции; проверим ее лишь для

.

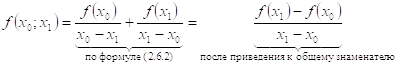Теорема 2.7. Пусть функция Имеет на отрезке , содержащем точки , производную порядка . Тогда справедливо равенство

(2.6.3)

Теорема 2.8. В случае когда таблица значений аргумента имеет постоянный шаг , конечная и разделенная разность связаны соотношением

(2.6.4)

Для доказательство теоремы очевидно.

< Предыдущая		Следующая >