04. Функция двух переменных. Линии уровня
Механизм работы с функцией нескольких переменных несколько отличается от механизма работы с функцией одной переменной. Например, как вычислить производную функции, если переменных больше, чем 1. В этом случае вводится понятие частных производных. При их вычислении пользуются следующим правилом: при вычислении частной производной функции по одной из переменных остальные переменные считаются константами, а в остальном механизм вычисления производной сохраняется. Например, определим частные производные функции:
![]()
При вычислении производной по первой переменной считаем константой вторую и наоборот.
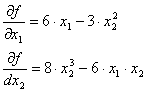
Понятие частной производной потребуется нам при вычислении предельной нормы замещения для производственной функции Кобба-Дугласа. Функция Кобба-Дугласа имеет вид
![]() ,
,
Где Y – объем выпускаемой продукции, x1 – трудозатраты, x2 – капитальные вложения, а A и a - некоторые постоянные коэффициенты производства, причем 0<a<1.
При исследовании функции Кобба-Дугласа нам необходимо будет, задавшись несколькими значениями выпуска продукции построить семейство линий уровня функции. Рассмотрим это на примере.
Пусть необходимо построить линии уровня функции Кобба-Дугласа для следующих значений выпуска продукции: Y1=10, Y2=20, Y3=30, A=5, a=0,4.
Так как уровень выпуска – величина постоянная – выразим x2 через x1 и построим таблицу соответствия.
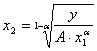
Зададимся значениями x1 от 10 до 100 с шагом 10 и определим значения x2 для каждого выпуска.
|
Y=10 |
Y=20 |
Y=30 | |
|
X1 |
X2 |
X2 |
X2 |
|
10 |
0,68399 |
2,171534 |
4,268272 |
|
20 |
0,430887 |
1,367981 |
2,688843 |
|
30 |
0,328828 |
1,043965 |
2,051971 |
|
40 |
0,271442 |
0,861774 |
1,693865 |
|
50 |
0,233921 |
0,742654 |
1,459728 |
|
60 |
0,207149 |
0,657657 |
1,292661 |
|
70 |
0,186918 |
0,593428 |
1,166416 |
|
80 |
0,170998 |
0,542884 |
1,067068 |
|
90 |
0,158084 |
0,501886 |
0,986485 |
|
100 |
0,147361 |
0,467843 |
0,919571 |
Теперь построим семейство линий уровня

По данному графику можно делать выводы о значениях и характере изменения капитальных вложений при изменении трудозатрат на данном уровне выпуска.
| < Предыдущая | Следующая > |
|---|