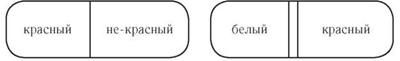03.2. Отношения между понятиями

Содержание понятия — совокупность тех свойств, которые при­сущи всем предметам, обозначаемым данным понятием, и только им.

К примеру, склероз — это, как известно, уплотнение каких-либо органов, вызванное гибелью специфических для этих органов элементов и заменой их соединительной тканью. Перечисленные свойства составля­ют содержание понятия «склероз». Они позволяют относительно любой ситуации решить, можно ли назвать происшедшие в органе изменения склерозом или нет. Содержание понятия «стул» составляют свойства быть предметом мебели, предназначенным для сидения, и иметь ножки, сиденье и спинку. Этими свойствами, относящимися к функциям стула и его строению, обладает каждый стул и не обладает ничто иное. Если изъять из числа структурных частей стула, скажем, спинку, получим со­держание уже иного понятия («табурет»). В содержание понятия «стол» входят признаки быть предметом мебели, предназначенным для сидения за ним, и иметь ножки и крышку.

Помимо содержания, или смысла, понятие имеет также объем.

Объем понятия — совокупность, или класс, тех предметов, которые обладают признаками, входящими в содержание понятия.

Например, в объем понятия «склероз» входят все случаи склеро­тического изменения органов, в частности склероз мозга. Объем поня­тия «стул» включает все стулья, объем понятия «стол» — все столы. Нетрудно заметить, что объемы даже таких простых понятий, как «стул» и «стол», являются неопределенными, размытыми, а значит, сами эти имена относятся к неточным.

Понятия находятся в различных отношениях друг к другу. Между объемами двух произвольных понятий, которые есть какой-то смысл со­поставлять друг с другом, имеет место одно и только одно из следующих отношений: равнозначность, пересечение, подчинение (два варианта) и исключение.

Равнозначность — отношение между понятиями, объемы которых полностью совпадают.

Иными словами, равнозначные понятия отсылают к одному и тому же классу предметов, но делают это разными способами. Равнозначны, к примеру, понятия «квадрат» и «равносторонний прямоугольник»: каж­дый квадрат является равносторонним прямоугольником, и наоборот.

Равнозначность означает совпадение объемов двух понятий, но не их содержаний. Например, объемы понятий «сын» и «внук» совпадают (каждый сын есть чей-то внук и каждый внук — чей-то сын), но содер­жания их различны.

Отношения между объемами понятий можно геометрически наглядно представить с помощью круговых схем. Они называются по имени мате­матика XVIII в. Л. Эйлера «кругами Эйлера». Каждая точка круга пред­ставляет один предмет, входящий в объем рассматриваемого понятия. Точки вне круга представляют предметы, не подпадающие под это по­нятие.

Равнозначность

Отношения между двумя равнозначными понятиями изображаются в виде двух полностью совпадающих кругов.

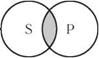
Пересечение — отношение между понятиями, объемы которых час­тично совпадают.

Пересечение

Пересекаются, например, понятия «летчик» и «космонавт»: некото­рые летчики являются космонавтами; некоторые летчики не космонавты; некоторые космонавты — не летчики.

Подчинение — отношение между понятиями, объем одного из кото­рых полностью входит в объем другого.

Подчинение

В отношении подчинения находятся, к примеру, понятия «треуголь­ник» и «прямоугольный треугольник»: каждый прямоугольный тре­угольник является треугольником, но не каждый треугольник — прямо­угольный.

В этом же отношении находятся имена «дедушка» и «внук»: каж­дый дедушка есть чей-то внук, но не каждый внук является дедушкой. «Внук» — подчиняющее имя, «дедушка» — подчиненное.

Подчиняющее понятие называется родом, а подчиненное — видом. Понятие «треугольник» есть род для вида «прямоугольный треуголь­ник», а понятие «внук» — род для вида «дедушка».

Исключение — отношение между понятиями, объемы которых пол­ностью исключают друг друга.

Исключение

Исключают друг друга понятия «трапеция» и «пятиугольник», «че­ловек» и «планета», «белое» и «красное» и т. п.

Можно выделить два интересных вида исключения:

1. Исключающие объемы дополняют друг друга так, что в сумме дают весь объем рода, видами которого они являются. Понятия, таким образом исключающие друг друга, называются противоречащими.

Противоречащими являются, например, понятия «умелый» и «не­умелый», «стойкий» и «нестойкий», «красивый» и «некрасивый» и т. п. Противоречат друг другу также понятия «простое число» и «число, не являющееся простым», исчерпывающие объем родового понятия «нату­ральное число», имена «красный» и «не являющийся красным», исчер­пывающие объем родового понятия «предмет, имеющий цвет», и т. п.

2. Исключающие понятия составляют в сумме только часть объема того рода, видами которого они являются. Такие понятия называются противоположными.

Противоречащие понятия Противоположные понятия

К противоположным относятся, в частности, понятия «простое чис­ло» и «четное число», не исчерпывающие объема родового понятия «на­туральное число», понятия «красный» и «белый», не исчерпывающие объема родового понятия «предмет, имеющий цвет» и т. п.

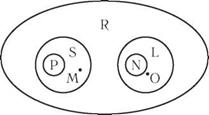
Круговые схемы могут применяться для одновременного представ­ления объемных отношений более чем двух понятий. Такова, к примеру, приведенная ниже схема, представляющая отношения между объемами понятий «планета» (S), «планета Солнечной системы» (Р), «Земля» (М), «спутник» (L), «искусственный спутник» (N), «Луна» (О) и «небесное тело» (R).

Согласно этой схеме, существуют, в частности, небесные тела, не являющиеся ни планетами, ни их спутниками, планеты, не входящие в Солнечную систему, спутники, не являющиеся искусственными, и т. д. Объемы единичных имен представляются точками.

< Предыдущая		Следующая >