10. Двойственный симплекс-метод (Р-Метод)

Пример 3.5. Рассмотрим следующую ЗЛП:

Min(2Х1 + 4Х2 )

3 Х1 + Х2 3

4 Х1 + 3 Х2 6 (3.63)

Х1 + 2 Х2 3

Х1,2 0

Приведем рассматриваемую ЗЛП к каноническому виду

Max (-2 Х1 -4 Х2 )

3 Х1 + Х2 - S1 = 3

4 Х1 + 3 Х2 - S2 = 6

Х1 + 2 Х2 - S3 = 3

или

max (-2 Х1 -4 Х2 )

- 3 Х1 - Х2 + S1 = - 3

- 4 Х1 - 3 Х2 + S2 = - 6 (3.64)

Х1 + 2 Х2+ S3 = 3

Рассмотрим расширенную матрицу системы линейных уравнений (3.64):

.

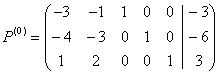Матрица Содержит единичную подматрицу порядка 3 и, следовательно, определяет базисное решение

= (-3; -6; 3); = (3; 4; 5)

Системы уравнений, причем = (0, 0, 0). Так как элементы (n + 1 = 6)-го столбца матрицы системы не являются неотрицательными, то она не является К-матрицей ЗЛП. Вычислим симплекс-разности матрицы :

, .

Так как все симплекс-разности матрицы являются неотрицательными, то базисное решение = (-3; -6; 3), не являющееся допустимым решением ЗЛП, является «лучшим», чем оптимальное решение.

При решении задачи симплекс-методом текущее базисное решение является допустимым, но неоптимальным. Эти соображения позволяют построить метод решения определенного класса ЗЛП. В этом методе, называемом двойственным симплекс-методом, на каждой итерации обеспечивается выполнение условия оптимальности текущего базисного решения, не являющегося допустимым. Критерием окончания процесса итераций является получение допустимого решения.

< Предыдущая		Следующая >