11. Условия перехода от одной р-матрицы ЗЛП к другой
Определение. Р-матрицей КЗЛП (3.18) будем называть расширенную матрицу системы линейных уравнений, равносильной системе (3.63), содержащую единичную подматрицу порядка m на месте n первых столбцов, все симплекс разности которой неотрицательны.
Очевидно, что всякая Р-матрица ЗЛП определяет некоторое базисное решение системы уравнений (3.63) (см. пример 3.5).
Определение. Базисное решение системы линейных уравнений (3.63), определяемое Р-матрицей, называется псевдопланом ЗЛП.
Пусть известна Р-матрица ![]() ЗЛП (3.18), определяющая псевдоплан
ЗЛП (3.18), определяющая псевдоплан
![]() =
=![]() ,
, ![]() .
.
Условия перехода от матрицы ![]() к матрице
к матрице ![]() Составляют содержание теоремы 3.12.
Составляют содержание теоремы 3.12.
Теорема 3.12. Пусть ![]() < 0 и в L-й строке матрицы
< 0 и в L-й строке матрицы ![]() Есть хотя бы один отрицательный элемент. Тогда с помощью одного шага метода Жордана–Гаусса можно построить новую Р-матрицу
Есть хотя бы один отрицательный элемент. Тогда с помощью одного шага метода Жордана–Гаусса можно построить новую Р-матрицу ![]() , выбрав направляющий элемент из условия
, выбрав направляющий элемент из условия
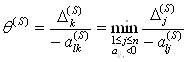 . (3.65)
. (3.65)
Замечание 1. Если в матрице ![]() Нет
Нет ![]() < 0, то определяемый ею псевдоплан является решением ЗЛП.
< 0, то определяемый ею псевдоплан является решением ЗЛП.
Теорема 3.13. Пусть ![]() < 0 и в L-й строке матрицы
< 0 и в L-й строке матрицы ![]() нет ни одного отрицательного элемента. Тогда множество планов Р ЗЛП (3.18) пусто.
нет ни одного отрицательного элемента. Тогда множество планов Р ЗЛП (3.18) пусто.
Замечание 2. При переходе от матрицы ![]() к матрице
к матрице ![]() Целевая функция изменяется в соответствии с формулой
Целевая функция изменяется в соответствии с формулой
F(![]() ) = F (
) = F (![]() ) +
) + ![]() = F (
= F (![]() ) +
) + ![]() , (3.66)
, (3.66)
Откуда следует, что
F (![]() )
)![]() F (
F (![]() ), (3.67)
), (3.67)
Так как ![]() < 0 и
< 0 и ![]() . Из неравенства (3.67) следует, что при переходе от одного псевдоплана к другому значение целевой функции
. Из неравенства (3.67) следует, что при переходе от одного псевдоплана к другому значение целевой функции ![]() не возрастает.
не возрастает.
| < Предыдущая | Следующая > |
|---|