09. Алгоритм Симплекс-метода
Будем считать, что известна исходная К-матрица К(0) задачи линейного программирования, определяющая исходный опорный план
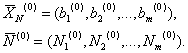
В симплексном методе последовательно строят К-матрицы
задачи линейного программирования, пока не выполнится критерий оптимальности или критерий, позволяющий убедиться в отсутствии конечного решения. Рассмотрим алгоритм S-й итерации симплексного метода. В начале S-й итерации имеем К-матрицу 
задачи линейного программирования, определяющую опорный план
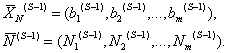
Шаг 1. Вычисляем для столбцов 
Матрицы 
симплекс-разности 
и находим номер k из условия 
.
Шаг 2. Если 
, то опорный план
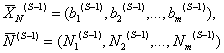
Является оптимальным, а
Есть оптимальное значение линейной формы 
, иначе переходим к шагу 3.
Шаг 3. Если 
, 
, то ЗЛП не имеет конечного решения, иначе находим номер L из условия
.
Направляющий элемент на S-й итерации метода есть элемент 
.
Шаг 4. Вычисляем компоненты вектора 
: 
Шаг 5. Производим один шаг метода Жордана–Гаусса с направляющим элементом . Присваиваем переменной S алгоритма значение S+1 и переходим к шагу 1.
Пример 3.3. Симплекс-методом решить ЗЛП:
(3.58)
Х1 + 2Х2 
6
2Х1 + Х2 8
-Х1 + Х2 1 (3.59)
Х2 £ 2
Х1 
0 Х2 0.
Приводим систему линейных неравенств (3.59) к каноническому виду, вводя в каждое неравенство дополнительную переменную Si , Где I = 1,4. Получим систему линейных уравнений:
Х1 + 2Х2 + S1 = 6
2Х1 + Х2 + S2 = 8 - Х1 + Х2 + S3 = 1 (3.60)
Х2 + S4 = 2
Целевая функция будет иметь вид 
= 3X1 + 2X2 + 0 S1 + 0 S2 + 0 S3 + 0 S4
Расширенная матрица 
Системы линейных уравнений (3.60) является исходной К-матрицей К(0) ЗЛП, которая определяет исходный опорный план:
, 
, 
.
Результаты последовательных итераций симплекс-алгоритма удобно оформить в виде симплексной таблицы.
Таблица 3.1
|
S |
I |
|
|
|
3
|
2
|
0
|
0
|
0
|
0
|
|
|
0 |
1 2 3 4 |
3 4 5 6 |
0 0 0 0 |
6 8 1 2 |
1 2 -1 0 |
2 1 1 1 |
1 0 0 0 |
0 1 0 0 |
0 0 1 0 |
0 0 0 1 |
6 4 - - |
|
5 |
|
|
-3 |
-2 |
0 |
0 |
0 |
0 |
K = 1 L = 2 | ||
|
1 |
1 2 3 4 |
3 1 5 6 |
0 3 0 0 |
2 4 5 2 |
0 1 0 0 |
3/2 1/2 3/2 1 |
1 0 0 0 |
-1/2 1/2 1/2 0 |
0 0 1 0 |
0 0 0 1 |
4/3 8 10/3 2 |
|
5 |
|
|
0 |
-1/2 |
0 |
3/2 |
0 |
0 |
K = 2 L = 1 | ||
|
2 |
1 2 3 4 |
2 1 5 6 |
2 3 0 0 |
4/3 10/3 3 2/3 |
0 1 0 0 |
1 0 0 0 |
2/3 -1/3 -1 -2/3 |
-1/3 2/3 1 1/3 |
0 0 1 0 |
0 0 0 1 | |
|
5 |
|
|
0 |
0 |
1/3 |
4/3 |
0 |
0 |
На второй итерации S = 2, все 
, следовательно, опорный план
,
Определяемый К-матрицей К(2), оптимальный, 
Оптимальное значение линейной формы равно:
.
Пример 3.4. Симплекс-методом решить ЗЛП:
max (2X1+X2) (3.61)
X1-X210
X140 (3.62)
X1,20
Приводим ЗЛП к каноническому виду
max (2X1+X2+0 S1+0S2)
X1-X2+ S1=10
X1+ S2=40
Результаты последовательных итераций записываем в симплекс-таблицу.
Таблица 3.2
|
S |
I |
|
|
|
2
|
1
|
0
|
0
|
|
|
0 |
1 2 |
3 4 |
0 0 |
10 40 |
1 1 |
-1 0 |
1 0 |
0 1 |
10 40 |
|
3 |
|
|
-2 |
-1 |
0 |
0 | |||
|
1 |
1 2 |
1 4 |
2 0 |
10 30 |
1 0 |
-1 1 |
1 -1 |
0 1 |
- 30 |
|
3 |
|
|
0 |
-3 |
2 |
0 | |||
|
2 |
1 2 |
1 2 |
2 1 |
40 30 |
1 0 |
0 1 |
0 -1 |
1 1 |
- - |
|
3 |
|
|
0 |
0 |
-1 |
3 |
Из симплекс-таблицы при S = 2 следует, что согласно шагу 3 симплекс-алгоритма данная ЗЛП не имеет конечного решения, т. к. отрицательная симплекс-разность 
Соответствует столбцу 
, все элементы которого неположительны.
Итак, 
.
| < Предыдущая | Следующая > |
|---|
