08. Переход от одной к-матрицы ЗЛП к другой к-матрице

Пусть известна К-матрица

. (3.45)

Обозначим через вектор номеров базисных (единичных) столбцов матрицы , – вектор, компоненты которого есть базисные компоненты опорного плана, определяемого матрицей , и могут быть отличны от нуля. Остальные (n-m) компонент опорного плана, определяемого матрицей , равны нулю. Очевидно, что векторы И Полностью задают опорный план, определяемый матрицей . Например, пусть

=,

Тогда = (3, 1, 6); == (1, 2, 4) и, следовательно, опорный план, определяемый , имеет вид

= (2, 0, 1, 0, 0, 4).

Итак, пусть К-матрица (3.45) определяет невырожденный опорный план

. (3.46)

Выберем в матрице Столбец , не принадлежащий единичной подматрице, т. е. , , и такой, что в этом столбце есть хотя бы один элемент больше нуля.

Пусть . Считая Направляющим элементом, совершим над матрицей один шаг метода Жордана–Гаусса. В результате получим новую матрицу

, (3.47)

В которой столбец стал единичным, но которая может и не быть К-матрицей, так как среди величин Могут быть отрицательные. Условия выбора направляющего элемента , позволяющие получить новую К-матрицу , т. е. обосновывающие способ перехода от опорного плана К опорному плану , составляют содержание следующей теоремы, которая была доказана выше:

Теорема 3.8 Пусть в K-м столбце К-матрицы - есть хотя бы один строго положительный элемент (,). Тогда с помощью одного шага метода Жордана–Гаусса можно построить новую К-матрицу , выбрав направляющий элемент из условия

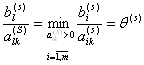. (3.48)

Определение. Величину

, (3.49)

Где – вектор, компонентами которого являются коэффициенты линейной функции при базисных () переменных опорного плана, определяемого матрицей , назовем j-й симплекс-разностью матрицы .

Если столбец является единичным в матрице , то =0.

Пусть и – опорные планы, определяемые матрицами и соответственно. Тогда очевидно, что

(3.50)

, (3.51)

Где k – номер столбца , вводимого в базис при получении матрицы из. Определяется по формуле (3.48).

Теорема 3.9. Пусть в матрице Есть И в столбце ( , ) есть хотя бы один строго положительный элемент. Тогда от матрицы Можно перейти к матрице , причем

F () F(). (3.52)

Доказательство.

Так как в столбце Матрицы есть строго положительный элемент, то согласно теореме 3.1 от матрицы можно перейти к новой матрице ЗЛП, выбрав направляющий элемент из условия (3.48).

Неравенство (3.52) вытекает из выражения (3.51), так как , а 0.

Теорема доказана.

Теорема 3.10. (критерий оптимальности опорного плана). Пусть все симплекс-разности матрицы Неотрицательные. Тогда опорный план , определяемый матрицей , является оптимальным.

Доказательство.

По условию теоремы

,

Или

. (3.53)

Пусть – произвольный план задачи линейного программирования. Умножим левую и правую части (3.53) на , тогда в силу неотрицательности получим

. (3.54)

Согласно (3.54) имеем

Или

,

Что и доказывает теорему.

Теорема 3.11. Пусть в матрице Есть и в столбце (,) нет ни одного строго положительного элемента. Тогда ЗЛП (3.18) не имеет конечного решения.

Доказательство.

Пусть k-я симплекс-разность матрицы

, (3.55)

И все

(3.56)

Матрица определяет опорный план

Рассмотрим вектор

У которого

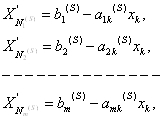
Где – любое положительное число.

Остальные Компонент вектора Положим равными нулю.

В силу условия (3.56) компонент вектора неотрицательные. Легко убедиться в том, что компоненты вектора удовлетворяют и функциональным ограничениям задачи линейного программирования, т. е. вектор – план задачи линейного программирования при любом положительном .

Имеем:

Или окончательно

(3.57)

Так как , то из (3.57) следует, что для любого числа Всегда можно найти план ЗЛП, для которого

Т. е. линейная форма Не ограничена сверху на множестве Планов.

Теорема доказана.

< Предыдущая		Следующая >