07. Решение линейных моделей Симплекс-методом

Рассмотрим каноническую задачу линейного программирования (КЗЛП):

(3.18)

Будем в дальнейшем считать, что ранг матрицы А системы уравнений равен m, причем m < n.

Запишем КЗЛП в векторной форме:

(3.19)

(3.20)

(3.21)

Где – j-й столбец матрицы А.

Определение. Опорным планом (ОП) задачи линейного программирования будем называть такой ее план, который является базисным решением системы линейных уравнений .

Согласно определению и предположению о том, что r(A) = m, всякому опорному плану задачи линейного программирования (как и всякому базисному решению системы линейных уравнений ) соответствует базисная подматрица В порядка m матрицы А и определенный набор m базисных переменных системы линейных уравнений .

Определение. m компонент базисного решения системы линейных уравнений , являющихся значениями соответствующих ему базисных переменных, будем называть базисными компонентами этого решения.

Отметим, что базисные компоненты опорного плана неотрицательны; остальные n-m его компонент равны нулю. Очевидно, что число опорных планов задачи линейного программирования конечно и не превышает . Число строго положительных компонент опорного плана не превышает m.

Определение. К-матрицей КЗЛП будем называть расширенную матрицу системы линейных уравнений, равносильной системе , содержащую единичную подматрицу на месте первых n своих столбцов и все элементы ( n+1 )-го столбца которой неотрицательны.

Число К-матриц конечно и не превышает . Каждая К-матрица определяет ОП КЗЛП и наоборот.

Теорема 3.2 (о крайней точке). Опорный план ЗЛП является крайней точкой множества P¢ и наоборот.

Доказательство.

Пусть вектор – опорный план ЗЛП, у которого компоненты Строго положительные, а остальные n-k компонент равны нулю.

Тогда согласно определению опорного плана ЗЛП векторы Линейно независимы.

Предположим, что вектор Не является крайней точкой множества P¢, то есть существуют векторы , и такие, что

. (3.22)

Векторы и – планы ЗЛП. Это означает, во-первых, что компоненты векторов и неотрицательные и вследствие (3.22) ровно k компонент вектора и ровно k компонент вектора могут быть строго положительными. Остальные n-k компонент каждого из векторов и Равны нулю.

Во-вторых, компоненты векторов и Удовлетворяют функциональным ограничениям (3.20) ЗЛП. Следовательно, имеют место следующие равенства:

Вычитая из первого равенства второе, получим

. (3.23)

Так как векторы линейно независимы, то из (3.23) следует, что или . Последнее означает, что = .

Получили противоречие, следовательно, – крайняя точка множества P¢.

Обратно, пусть теперь вектор – крайняя точка множества P¢, строго положительными компонентами которой являются . Так как вектор – план ЗЛП, то его компоненты удовлетворяют функциональным ограничениям (3.20) задачи, то есть имеет место равенство

(3.24)

Предположим, что вектор Не является опорным планом ЗЛП. Тогда согласно определению опорного плана ЗЛП векторы Линейно зависимы, то есть существуют такие действительные числа, , не все равные нулю, что

(3.25)

Зададим некоторое ε > 0. Умножим левую и правую части равенства (3.25) сначала на ε, затем на (-ε). Каждое из полученных равенств сложим с (3.24), в результате получим

(3.26)

(3.27)

Выберем ε настолько малым, чтобы выполнялись неравенства

, (3.28)

.

Рассмотрим векторы и , у каждого из которых отличными от нуля могут быть лишь k компонент

И

Соответственно, а остальные n-k компонент равны нулю.

Согласно (3.26) – (3.28) векторы и являются планами ЗЛП.

Имеем , то есть лежит внутри отрезка, соединяющего две различные точки и Множества P’.

Последнее означает, что – не крайняя точка множества P¢. Получили противоречие, следовательно, – опорный план ЗЛП.

Теорема доказана.

Следствие 1. Крайняя точка множества P¢ может иметь не более m строго положительных компонент.

Следствие 2. Число крайних точек множества P¢ конечно и не превышает .

Следствие 3. Если множество P¢ ограниченное, то оно является выпуклым многогранником.

Теорема 3.3 (о существовании опорного плана или решения ЗЛП). Если линейная форма Ограничена сверху на непустом множестве P¢, то ЗЛП разрешима, то есть существует такая точка , что .

Теорема 3.4. Если множество P¢ не пусто, то оно имеет опорный план (или крайнюю точку).

Доказательство.

Заметим, прежде всего, что если правые части bi (i = 1, 2,…, m) системы линейных уравнений равны нулю, то, так как ранг матрицы А равен m, вектор Является вырожденным опорным планом задачи линейного программирования. Поэтому в дальнейшем будем предполагать, что среди bi есть отличные от нуля.

Пусть вектор – план, но не опорный план задачи линейного программирования с k строго положительными компонентами. Не нарушая общности, будем считать, что строго положительными являются первые k компонент вектора , тогда имеет место равенство

. (3.29)

Так как вектор – не опорный план, то согласно определению опорного плана ЗЛП векторы линейно зависимы, то есть существуют действительные числа , не все равные нулю и такие, что

. (3.30)

Введём обозначение

(3.31)

Изменением знака в (3.30) можно всегда добиться, чтобы μ было положительным.

Умножим левую и правую части (3.30) на и полученное равенство сложим с (3.29), будем иметь

Или, так как

В силу (3.31) (3.33)

И обязательно существует такое j, для которого в соотношении (3.33) имеет место равенство.

Положим для определённости, что .

Таким образом, мы построили план задачи линейного программирования, j-я компонента которого есть , а остальные n – k + 1 компонент равны нулю.

Если при этом векторы оказались линейно зависимыми, то, рассуждая аналогично, получим план задачи линейного программирования, у которого k – 2 строго положительных компонент и так далее до тех пор, пока не построим такой план задачи линейного программирования с L (L ≤ K) строго положительными компонентами, что соответствующие этим компонентам векторы будут линейно независимыми. Так по предложению среди bi есть отличные от нуля, то L ≠ 0.

Согласно определению опорного плана ЗЛП построенный план является при L = M невырожденным, а при L < M вырожденным опорным планом задачи линейного программирования.

Теорема доказана.

Теорема 3.5. Пусть векторы `X1 , `X2 , …,`XN – планы задачи линейного программирования. Тогда вектор

(3.34)

Где

(3.35)

Будет решением задачи линейного программирования тогда и только тогда, когда её решением является каждый из векторов

Доказательство.

Пусть каждый из векторов является решением задачи линейного программирования, то есть

Тогда , то есть вектор определяемый соотношениями (3.34) и (3.35), также является решением задачи линейного программирования.

Обратно, пусть вектор , где является решением задачи линейного программирования.

Предположим, что среди векторов Есть хотя бы один вектор , который не является решением задачи линейного программирования, то есть имеет место следующее неравенство:

(3.36)

Тогда, учитывая (3.35), будем иметь

.

Получили противоречие, следовательно, каждый из векторов Есть решение задачи линейного программирования.

Теорема доказана.

Можно доказать следующую теорему о существовании оптимального опорного плана, или опорного решения, задачи линейного программирования.

Теорема 3.6. Пусть вектор Является решением задачи линейного программирования. Тогда существует опорный план, на котором функция Достигает своего глобального максимума.

Доказательство.

Заметим, что так как по условию теоремы множество планов P¢ не пусто, то согласно теореме 3.4 оно имеет хотя бы одну крайнюю точку.

Рассмотрим 2 случая:

1. Пусть Р¢ – выпуклый многогранник, а – решение задачи линейного программирования. Тогда согласно теореме, которая гласит, что любая точка выпуклого замкнутого ограниченного множества К может быть представлена в виде выпуклой линейной комбинации конечного числа крайних точек этого множества,

, , (3.37)

Где - крайние точки множества Р¢.

Выбросим из системы крайних точек те, которые входят в разложение (3.37) с коэффициентом αi = 0. Пусть это будут точки

.

Тогда

,

Т. е. выполняются условия теоремы 3.5 и, следовательно,

,

что и доказывает теорему.

2. Пусть Р¢ – неограниченное множество, а – конечное решение задачи линейного программирования.

Тогда можно указать такое положительное число М, что

. (3.38)

Введём в задачу линейного программирования дополнительное функциональное ограничение

(3.39)

И рассмотрим новую задачу линейного программирования

(3.40)

При условиях

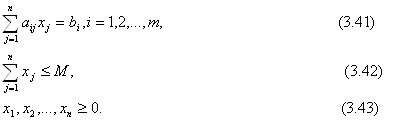
Множество планов данной задачи обозначим Р¢¢. Множество Р¢¢ – ограниченное, а так как компоненты вектора Удовлетворяют условиям (3.41) – (3.43) и , то Является решением задачи. Следовательно, согласно доказанному в случае 1 во множестве Р¢¢ существуют крайние точки такие, что

,

Причём

, (3.44)

Если бы хотя бы одна крайняя точка (I = 1, 2,…, N) не принадлежит гиперплоскости

,

То она является крайней точкой множества Р¢ и теорема доказана.

Пусть все крайние точки (I = 1, 2,…, N) принадлежат гиперплоскости

, то имеют место равенства

.

Тогда из (3.44) имеем

Что противоречит условию (3.38) выбора М > 0.

Теорема доказана.

Теорема 3.7. (следствие теоремы 3.5) Если решение задачи линейного программирования достигается в нескольких крайних точках области Р¢, то оно достигается и в любой выпуклой линейной комбинации этих точек.

Пусть требуется решить задачу (3.18). Так как по доказанному выше решением задачи (3.18) является неотрицательное базисное решение системы линейных уравнений , то метод решения задачи (3.18) должен содержать четыре момента:

1) обоснование способа перехода от одного опорного плана (К-матрицы) к другому;

2) указание признака оптимальности, позволяющего проверить, является ли данный опорный план оптимальным;

3) указание способа построения нового опорного плана, более близкого к оптимальному;

4) указание признака отсутствия конечного решения.

< Предыдущая		Следующая >