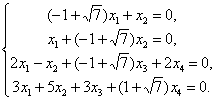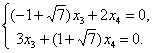30. Собственные векторы и собственные значения линейного преобразования
Пусть LN – линейное n-мерное пространство над полем Р, J : Ln ® Ln – линейное преобразование и А –матрица этого преобразования в некотором базисе Е.
Определение 40. Ненулевой вектор А называется Собственным вектором преобразования J, если J(А) = L×А для некоторого L Î Р. Элемент l называется Собственным значением Преобразования J.
По определению собственного вектора, А – собственный вектор преобразования J Û $L Î Р : J(А) = L×А. Перепишем это равенство в координатах, получим А×Х = L×Х. Отсюда А×Х – (LЕ)×Х = О, или (А –LЕ)×Х = О. Итак, А – собственный вектор преобразования J Û столбец координат этого вектора является ненулевым решением уравнения (А –LЕ)×Х = О (38). Матрица (А –LЕ) Называется Характеристической матрицей для матрицы А. Матричное уравнение (38) перепишем в виде системы уравнений. Получим, что А – собственный вектор
|
|
Преобразования J Û (Х1, х2, … , хn ) – ненулевое решение системы (39), при этом все Хк Принадлежат полю Р. Так как (39) система линейных однородных уравнений и число уравнений равно числу неизвестных, то она имеет ненулевое решение тогда и только тогда, когда её определитель равен нулю, т. е. |
|
|
Имеет место равенство (40). Уравнение (40) называется Характеристическим уравнением Матрицы А. Определитель системы, т. е. | А – LЕ |, называется Характеристическим Многочленом матрицы А. |
Корни характеристического многочлена называются Характеристическими корнями матрицы А. ( Характеристический корень не всегда принадлежит полю Р). Множество всех характеристических корней матрицы А называется её Спектром.
Согласно определению 40, L Î Р. Пусть L0 Î Р И является характеристическим корнем матрицы А. При L0 система (39) имеет ненулевое решение, т. е. J Будет иметь собственный вектор и L0 Будет собственным значением преобразования J, заданного матрицей А.
Теорема 37. Характеристические многочлены подобных матриц одинаковы.
Доказательство. Пусть В = С–1×А×С. Так как матрица LЕ Перестановочна с любой матрицей, то | В – LЕ | = | С–1×А×С – LЕ | = | С–1×А×С – С–1 ×(LЕ)×С | = | С–1×(А – LЕ)×С | = |С–1 || А – LЕ ||С| = | А – LЕ |.
Так как матрицы линейного преобразования в разных базисах подобны, то
Следствие. Матрицы линейного преобразования в разных базисах имеют один и тот же спектр.
Определение 41. Спектр матрицы линейного преобразования в каком-нибудь базисе называется Спектром линейного преобразования.
Теорема 38. Собственными значениями линейного преобразования J : Ln ® Ln , действующего в линейном пространстве над полем Р, являются характеристические корни этого преобразования, принадлежащие полю Р, и только они.
Доказательство Этой теоремы вытекает из всего сказанного выше.
Можно сформулировать следующие правила нахождения собственных значений и собственных векторов линейного преобразования.
1. Записать матрицу данного преобразования в некотором базисе.
2. Составить характеристическое уравнение и найти его корни, принадлежащие полю Р (т. е. найти собственные значения).
3. Если L0 – собственное значение, то составить систему  и найти её ненулевые решения.
и найти её ненулевые решения.
Пример. Найти собственные значения и собственные векторы линейного преобразования J : L4 ® L4 (над полем R), если это преобразование в базисе Е = (Е1, Е2, е3,Е4) имеет матрицу А.
|
А = |
Решение. Составим характеристическое уравнение (*). Используя теорему Лапласа, раскроем определитель, получим уравнение: |
|
![]() , [(1 – L )2 – 1]×[(1– L )×(3 –L ) – 6] = 0. Возможны два случая:
, [(1 – L )2 – 1]×[(1– L )×(3 –L ) – 6] = 0. Возможны два случая:
1) (1 –L )2 – 1 = 0, 1 – L = ± 1. Отсюда L1 = 0, L2 = 2.
2) (1– L )×(3 –L ) – 6 = 0, L2 – 4L – 3 = 0, L3 = ![]() , L4 =
, L4 = ![]() . Итак, характеристическое уравнение имеет четыре корня, все они действительные. Поэтому данное преобразование имеет четыре собственных значения. Для каждого из них составим систему уравнений для нахождения собственных векторов.
. Итак, характеристическое уравнение имеет четыре корня, все они действительные. Поэтому данное преобразование имеет четыре собственных значения. Для каждого из них составим систему уравнений для нахождения собственных векторов.
|
1) При L = 0. |
Отсюда Х2 = – х1. Подставим в третье и четвёртое уравнения, получим
|
Решив последнюю систему, получим Х4 = ![]() , х3 =
, х3 = ![]() . Если Х1 = 3С, То Х2 = –3С, Х3 = 13С, х4 = –11С, С – любое действительное число, отличное от нуля. Итак, собственными векторами, принадлежащими собственному значению L = 0, являются все ненулевые векторы вида (3С, –3С, 13С, –11С ).
. Если Х1 = 3С, То Х2 = –3С, Х3 = 13С, х4 = –11С, С – любое действительное число, отличное от нуля. Итак, собственными векторами, принадлежащими собственному значению L = 0, являются все ненулевые векторы вида (3С, –3С, 13С, –11С ).
|
2) При L = 2. |
Отсюда Х2 = х1. Подставим в третье и четвёртое уравнения.
|
Решив последнюю систему, получим Х3 = ![]() , Х4 =
, Х4 = ![]() Если Х1 = 7С, то Х2 = 7С, х3 = –15С, х4 = –11С, Где С – любое отличное от нуля действительное число. Итак, собственными векторами, принадлежащими собственному значению L = 2, являются все ненулевые векторы вида (7С, 7С, –15С, –11С ).
Если Х1 = 7С, то Х2 = 7С, х3 = –15С, х4 = –11С, Где С – любое отличное от нуля действительное число. Итак, собственными векторами, принадлежащими собственному значению L = 2, являются все ненулевые векторы вида (7С, 7С, –15С, –11С ).
|
3) При L = |
Из первых двух уравнений Х1 = х2 = 0. Подставив в третье и четвёртое уравнения, получим
|
|
Из этой системы | |
|
4) При L = |
Из первых двух уравнений Х1 = х2 = 0 . Подставив в третье и четвёртое уравнения, получим
|
|
Из полученной системы |
Свойства собственных векторов.
10. Если вектор А – собственный вектор преобразования j, принадлежащий собственному значению l и A ¹ 0, то A×А – тоже собственный вектор, принадлежащий тому же собственному значению.
Если J (А ) = LА, то J(AА) =AJ(А) = A(LА) = L(AА).
20. Множество всех собственных векторов линейного преобразования J : Ln ® Ln , принадлежащих одному и тому же собственному значению (если к ним добавить нулевой вектор), есть линейное подпространство в Ln .
Пусть А И в два собственных вектора и J(А ) = LА, J(В) = LВ. Тогда J(AА + BВ) = AJ(А) + BJ(В) = A(LА) + B(LВ) = L(AА + BВ).
30. Собственные векторы, принадлежащие различным собственным значениям, линейно независимы.
Пусть J(А ) = LА, J(В) = L1В, L ¹ L1. Если бы А И в были бы линейно зависимы, то хотя бы один из них линейно выражался через другой пусть В = AА. Так как В – собственный вектор, то A ¹ 0. Тогда J(В) = J(AА). Отсюда L1В = A(LА), L1(AА) = A(LА), A(L1 – L)А = 0. Но в левой части A ¹ 0, L1 – L ¹ 0, А ¹ 0. Противоречие. Следовательно, А И в – линейно независимы.
40. Если в базисе Е = (Е1, Е2, ... , Ек, … , Еn ) вектор Ек – собственный вектор линейного преобразования J, принадлежащий собственному значению L, то в К-ом столбце матрицы этого преобразования на всех местах, кроме К-го, стоят нули и Акк = L.
| < Предыдущая | Следующая > |
|---|
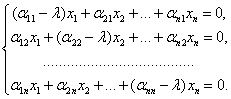 (39)
(39) (40)
(40)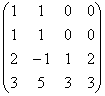 .
.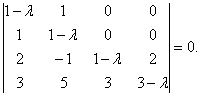 (*)
(*)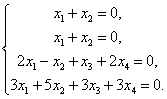
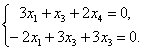 Отсюда
Отсюда 
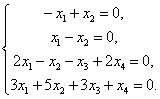
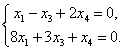 Отсюда
Отсюда