27. Связь матриц линейного оператора в разных парах базисов

Пусть даны два линейных пространства Ln и Lm над полем Р. Пусть в Ln зафиксированы базисы Е = (Е1, Е2, … , Еn ) и Е1 = (Е11, Е21, … , Еn1 ), а в пространстве Lm – базисы F = (f1, f2, … , fm ) и F1 = (f11, f21, … , fm1 ). Пусть J: Ln ® Lm линейный оператор, А – его матрица в паре базисов Е и F и А1 – матрица этого же оператора в паре базисов Е1 и F1. Пусть Т – матрица перехода от базиса Е к базису Е1, а Q – матрица перехода от F к F1. Тогда Е1 = Е×Т, F1 = F×Q , J(Е) = F×А , J(Е1) = F1×А1. Отсюда J( е×Т) = ( F×Q )×А1, J(Е)×Т = F×(Q ×А1). Так как Т – матрица перехода, то она невырожденная, следовательно, существует матрица Т–1. Из последнего равенства получаем, что J(Е) = ( F×(Q ×А1))×Т–1 = F×(Q ×А1×Т–1). Но J(Е) = F×А. Следовательно, А = Q ×А1×Т–1, или А1 = Q–1 ×А×Т (34)

Пример. Даны два линейных пространства L3 И L5 . Пусть Е = (Е1, Е2, е3) и F = (f1, f2, f3 , f4 , f5 ) – базисы в L3 И L5 соответственно. Пусть А1 = (1, 4, –1, 3, 0), А2 = (3, 0, 1, –3, 7), А3 = (1, 1, 2, 2, 0) – три вектора из L5 . Пусть линейный оператор J: L3 ® L5 задан по правилу J(Х1Е1 + Х2Е2 + Х3Е3 ) = Х1А1 + Х2А2 + Х3А3. Составить матрицу оператора J и найти образ вектора С = (5, –1, 3).

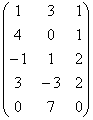
Решение. Для составления матрицы оператора достаточно найти координаты образов базисных элементов пространства L3 в базисе F пространства L5 . По данному правилу получим J(Е1) = 1×А1 = (1, 4, –1, 3, 0), J(Е2) = 1×А2 = (3, 0, 1, –3, 7), J(Е3) = 1×А3 = (1, 1, 2, 2, 0). Составим матрицу, столбцами которой являются координаты найденных векторов.

А =

Координаты вектора J(С) Можно найти по формуле (33), а именно, Х1 = А×Х .

× = .

Итак, J(С) = (5, 23, 0, 24, -7) в пространстве L5 . (Сравните с решением этого же примера в пункте 6.1.)

< Предыдущая		Следующая >