22. Связь решений однородной и неоднородной систем линейных уравнений
Пусть 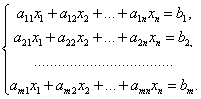 (25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется Соответствующей однородной системой (это система (30)). Решения систем (25) и (30) удовлетворяют следующим свойствам:
(25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется Соответствующей однородной системой (это система (30)). Решения систем (25) и (30) удовлетворяют следующим свойствам:
|
|
10. Сумма решений данной неоднородной и соответствующей однородной системы линейных уравнений есть решение данной неоднородной системы. Пусть А – частное решение системы (25) и С – частное решение системы (30). Рассмотрим вектор (А + С). |
Системы (25) и (30) в векторной форме имеют вид А×Х = В (31) и А×Х = 0 (32). По условию А×А = В, А×С = 0. Следовательно, А×(А + С) = А×А + А×С = В + 0 = В. Следовательно, (А + С) – решение уравнения (31), а поэтому и системы (25).
20. Разность двух решений неоднородной системы линейных уравнений есть решение соответствующей однородной системы.
Пусть А И С – Решения системы (25), а следовательно, и уравнения (31), т. е. А×А = В И А×С = В. Тогда А×(А – с) = А×А – А×С = В – в = 0, т. е. (А – с) – решение уравнения (32), а поэтому и системы (30).
30. Если А – фиксированное частное решение системы (25), а С пробегает все решения системы (30), то (А + С) пробегает все решения системы (25).
Согласно 10, при любом С Вектор (А + С) будет решением системы (25). Если D – любое решение системы (25), то, согласно 20, разность (D – А) будет решением системы (30). Обозначив (D – А) = С, получим D = (А + С).
Теорема 29. Если А – частное решение линейной неоднородной системы уравнений и А1, а2, …, аn–r – фундаментальная система решений соответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид
D = а + С1А1 + С2А2 + … + Сn–r Аn–r , где С1, С2, … , Сn–r – любые элементы поля Р.
(Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.)
Доказательство Является следствием предыдущих свойств.
| < Предыдущая | Следующая > |
|---|
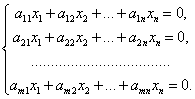 (30)
(30)