21. Пространство решений системы линейных однородных уравнений
Пусть дана система (30) линейных однородных уравнений с коэффициентами из поля Р.
|
|
Так как столбец свободных членов в матрице А1 этой системы состоит только из нулей, то rang A = rang A1, т. е. система линейных однородных уравнений всегда совместна. В частности она всегда имеет нулевое решение. Рассмотрим множество всех возможных решений системы (30). |
Пусть A =(A1, A2, … , An) и B =(B1, B2, … , Bn) – Любые два из них. Их можно рассматривать, как векторы в арифметическом n-мерном пространстве над полем Р. Пусть L – любой элемент поля Р. Тогда A +B = (A1 + B1, A2 + B2, … , An + Bn ), L×A = (LA1, LA2, … , LAn). Подставим компоненты этих векторов в произвольное S-е уравнение системы (30). Получим ![]()
![]() Итак, если A и B – Любые два решения системы (30) и L – любой элемент поля Р, то A +B И L×A тоже являются решением этой системы. Но тогда из теоремы 14 следует
Итак, если A и B – Любые два решения системы (30) и L – любой элемент поля Р, то A +B И L×A тоже являются решением этой системы. Но тогда из теоремы 14 следует
Теорема 27. Множество решений системы линейных однородных уравнений с N Переменными есть линейное подпространство арифметического пространства Аn .
Теорема 28. Размерность пространства решений системы линейных однородных уравнений равна N – r, Где N – Число неизвестных, r – ранг матрицы системы.
Доказательство. Пусть L – пространство решений системы (30). Тогда L Ì Аn . Пусть A = (A1, A2, … Ar, Ar+1, … , An) – произвольное решение системы. Пусть (Ar+1, … , An) – набор свободных неизвестных, соответствующий этому решению. Множество всех возможных наборов свободных неизвестных есть арифметическое (N – r)-мерное пространство Аn–r . Зададим отображение J: L ® Аn–r по правилу
A = (A1, A2, … Ar, Ar+1, … , An) ® J(A) = (Ar+1, … , An).
Покажем, что J – изоморфизм (определение 24). Для этого нужно проверить три условия.
1. Покажем, что J – взаимнооднозначное отображение. Решению A = (A1, A2, … Ar, Ar+1, … , An) соответствует только один набор (Ar+1, … , An), следовательно, J – Однозначное отображение. Обратно, если задать элемент (Ar+1, … , An) из Аn–r , то по теореме Крамера найдётся только один набор (A1, A2, … Ar ) искомых неизвестных, т. е. каждый элемент J(A) из Аn–r соответствует единственному элементу из L .
2. J(LA) = (LAr+1, … , LAn ) = L×(Ar+1, … , An ) = L×J(А).
3. J(А + В) = (AR+1 + BR+1, … ,AN + BN ) = (Ar+1, … , An) + (BR+1, … , BN ) = J(А) + J(В).
Итак, пространство решений системы линейных однородных уравнений изоморфно арифметическому (N – r)-мерному пространству. Следовательно, размерность L равна (N – r).
Определение 29. Базис пространства решений системы линейных однородных уравнений называется её Фундаментальной системой решений.
Так как при изоморфизме базис пространства Аn–r соответствует базису пространства L , То для того. чтобы найти фундаментальную систему решений для системы (30), достаточно выбрать (N – r) линейно независимых наборов свободных неизвестных и для каждого из них найти решение данной системы.
Следствие. Если А1, а2, …, аN–r фундаментальная система решений системы линейных однородных уравнений (30) и С1, С2, … , СN–r – произвольные элементы поля Р, то С1А1 + С2А2 + … + СN–r АN–r – общее решение этой системы.
| < Предыдущая | Следующая > |
|---|
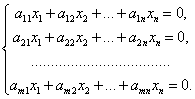 (30)
(30)