16. Матрица перехода. Связь координат вектора в разных базисах
Пусть L – линейное пространство над полем Р и пусть в нём зафиксированы два базиса Е = (Е1, Е2, … , Еn ) и Е1 = (Е11, Е21, … , Еn1 ). Пусть
|
|
Если ввести матрицу Т = |
То систему (23) можно записать в матричном виде Е1 = е×Т (24). |
Матрица Т называется Матрицей перехода от базиса Е К базису е1. Так как векторы Е11, Е21, … , Еn1 линейно независимы, то матрица Т невырожденная.
Если вектор А В базисе Е имеет координаты Х = (A1, A2, … , An)Т, а в базисе Е1 Его координаты Х1 = (B1, B2,…, Bn)Т, то А = Е×х и А = Е1×х1. отсюда Е×х = Е1×х1. Используя формулу (24), получим Е×х = (Е×Т)×Х1 = Е× (Т×х1). Отсюда Х = Т×х1 (25). Формула (25) даёт связь координат одного и того же вектора в разных базисах. Её называют формулой преобразования координат.
Пример. Пусть Е = (Е1, Е2, е3 , Е4 ) – базис в пространстве L4. Пусть Е11 = 2Е1 – 3Е3 , Е21 = е2 + Е4 , Е31 = 4Е1 + Е2 – Е4 , Е41 = Е2 + 3Е3 – Е4 ; Е111 = Е1 + Е2 , Е211 = Е1 – е3 , Е311 = Е3 + Е4 , Е411 = Е3 – е4 . Покажите, что Е1 = (Е11, Е21, … , Еn1 ) и Е11 = (Е111, Е211, … , Еn11 ) являются базисами в L.. Вектор А в базисе Е1 имеет координаты (1, 4, –2, 5). Найдите координаты этого вектора в базисе Е11.
Решение. Составим определители матриц перехода Т1 И Т2 от базиса Е К Е1 И Е11 соответственно.
|
|Т1| = |
|Т2| = |
|Т1|= |
|Т2| = 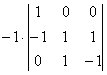 = 2. Так как матрицы Т1 И Т2 невырожденные, то Е1 И е11 – базисы.
= 2. Так как матрицы Т1 И Т2 невырожденные, то Е1 И е11 – базисы.
Из формулы (25) следует Х = Т1×Х1, х = Т2×х11. Отсюда Т1×х1 = Т2×х11, Х11 = (Т2-1×Т1)×Х1.
Найдём Т2-1. Для этого вычислим все алгебраические дополнения элементов матрицы Т2.
А11= 0, А12 = –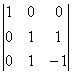 = 1, А13 =
= 1, А13 = 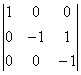 = 1, А14 = –
= 1, А14 = – = 1, А21 = –
= 1, А21 = –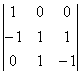 , А22 =
, А22 =  = –2, А23 = –
= –2, А23 = –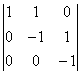 = –1, А24 =
= –1, А24 = 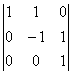 = –1, А31 =
= –1, А31 = 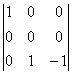 = 0, А32 = –
= 0, А32 = – = 0, А33 =
= 0, А33 = 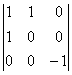 = 1, А34 = –
= 1, А34 = –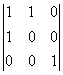 = –1, А41 = –
= –1, А41 = –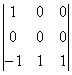 = 0, А42 =
= 0, А42 = 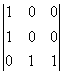 = 0. А43 = –
= 0. А43 = –  = 1, А44 =
= 1, А44 =  = –1. Используя найденные алгебраические дополнения, получим Т2-1 =
= –1. Используя найденные алгебраические дополнения, получим Т2-1 =  . Следовательно,
. Следовательно, ![]() =
= 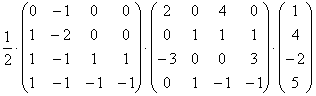 =
= ![]() . Итак, в базисе Е11 данный вектор имеет координаты (
. Итак, в базисе Е11 данный вектор имеет координаты ( ![]() –10; 0; –17).
–10; 0; –17).
| < Предыдущая | Следующая > |
|---|
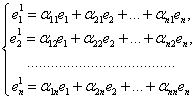 (23)
(23) ,
, ,
, ,
, =–12
=–12