09. Умножение матриц

Пусть А – матрица размерности M´n и В – матрица размерности N´ к. Произведением матрицы А на матрицу В называется матрица С, элементы которой получаются следующим образом: каждый элемент Р-ой строки матрицы А Умножается на соответствующий элемент Q-Го столбца матрицы В, Полученные произведения складываются и результат ставится в пересечение Р-Ой строки и q-Го столбца матрицы С, т. е. Срq = (11).

Размерность матрицы С Равна M´ к.

Пример 1.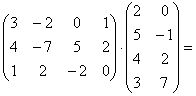

= .

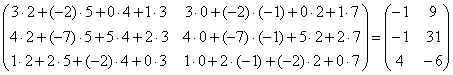Пример 2. Произведение матриц 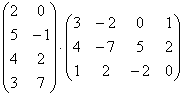не определено.

Но даже если А×В И В×А определены, то они не обязаны быть равны.

Пример 3. А×В = ,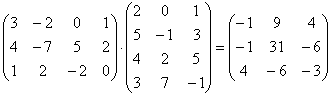

А×В = .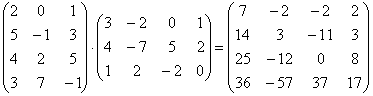

В этом примере А×В и В×А определены, но А×В ¹ В×А . Следовательно, для умножения матриц коммутативный закон не имеет места. Можно проверить:

10. Если (А×В)×С И А×(В×С) определены, то (А×В)×С = А×(В×С).

20. Если (А + В)×С Определено, то (А + В)×С = А×С + В×С.

30. Если А×В определено, то (lА)×В =L×(А×В).

< Предыдущая		Следующая >